I played WMCTF 2020 in mixed team of Defenit and zer0pts named Defenitelyzer0. We got 8th place!
Thanks to my team members.

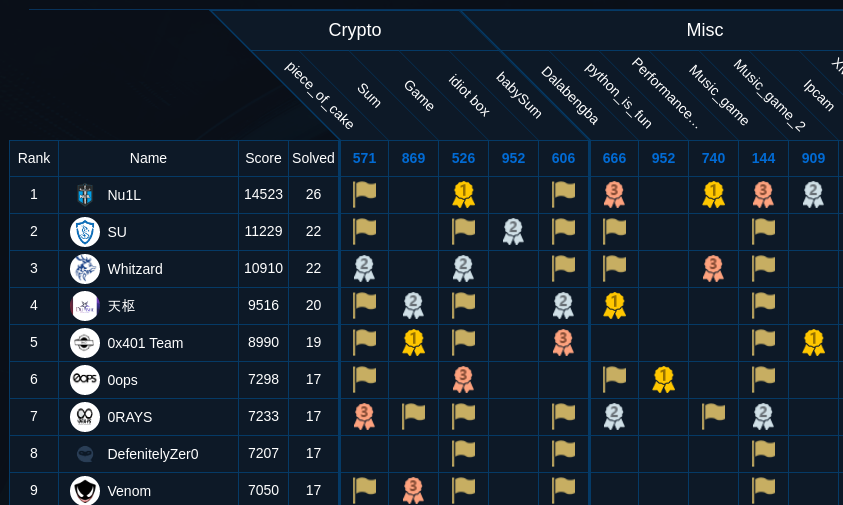
I tried to solve the crypto challenges, but they are too hard for me. I could solve only one challenge. I wanted to solve the piece_of_cake.

[Crypto: 606pts] babySum (14 solved)

We are given some scripts. The data contained a single number s and a list of 120 numbers A. We can load in json format.
Reading check.py, we will see that we need to solve a typical subset sum problem.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

from json import load

k, n, d = 20, 120, 0.8
s, A = load(open("data", "r"))

while True:
    inp = input("Please input the solution (seperated by comma): ") # <- 0, 1, 0, 1, ...
    sol = [int(i) for i in inp.split(',')]

    assert len(sol) == n
    assert all(i == 0 or i == 1 for i in sol)
    assert sum(i == 1 for i in sol) == k
    if sum(x*a for x, a in zip(sol, A)) == s:
        m = int(''.join(str(i) for i in  sol), 2)
        print(f"TQL! flag is {str(m).join(['WMCTF{', '}'])}")
        break

Also, reading task.py, the density of A is 0.8 so we can solve with a lattice basis reduction.
First, I tried CLOS method with LLL, but it was not working well. So I used BKZ algorithm. BKZ is more powerful but slower than LLL. I had to wait a long time for calculating.
Let $ N = \sqrt{n} $ , we can reduce the following lattice.
$$ \displaystyle \begin{pmatrix} 1 & 0 & \cdots & 0 & a _ {0} N & N\\ 0 & 1 & \cdots & 0 & a _ {1} N & N\\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & a _ {n} N & N\\ 0 & 0 & \cdots & 0 & sN & kN \end{pmatrix} $$ By the (n+2)th column, we can bind the number of numbers in the subset sum to k.
Moreover, simply running the BKZ algorithm on this matrix may not work well, so we can shuffle the lines and repeat.
Here is the solver written in sage.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

from json import load

def chk(sol, A, s):
    return sum(x * a for x, a in zip(sol, A)) == s

def solve(A, n, k, s, BS=22):
    N = ceil(sqrt(n))

    lat = []
    for i, a in enumerate(A):
        lat.append([(j == i) for j in range(n)] + [N * a] + [N])
    lat.append([0] * n + [N * s] + [k * N])

    cnt = 0
    while True:
        cnt += 1

        l = lat[::]
        shuffle(l)

        m = matrix(ZZ, l)
        bkz = m.BKZ(block_size=BS)
        print("{}".format(cnt))

        for i, row in enumerate(bkz):
            if chk(row, A, s):
                if row.norm() ** 2 == k:
                    print("find: {}".format(row[:-2]))
                    return

k, n, d = 20, 120, 0.8
s, A = load(open("data", "r"))
solve(A, n, k, s)

It takes about 30 minutes to get the results. We can get a flag by putting the result in check.py. WMCTF{83077532752999414286785898029842440}