セキュリティキャンプ応募課題晒し (2023, L1 暗号化通信ゼミ)

$$ \gdef\F{\mathbb{F}} \gdef\Z{\mathbb{Z}} \gdef\End{\mathrm{End}} \gdef\cl{\mathrm{cl}(\Z[\pi])} \gdef\ell{\mathcal{Ell} _ p (\Z[\pi],\pi)} \gdef\a{\mathfrak{a}} \gdef\b{\mathfrak{b}} \gdef\l{\mathfrak{l}} \gdef\O{\mathcal{O}} $$

はじめに

　どうも，mitsu です．今までなんやかんや忙しくて参加できないでいたセキュリティキャンプに，ついに今年は幸運にも参加することができました．

　興味のあるゼミはいくつかありましたが，とんでもなく強い講師の方々がいらっしゃるのでせっかくだからと自分の一番興味のある部分をさらに伸ばそうと思い L1（暗号化通信ゼミ）のプリミティブコースに応募しました．

　より具体的に言うと，Castryck と Decru によって 2022 年の夏頃に SIDH（更に正確には SIKE）を破る論文が出されちょうどそれを読んでいたのですがあまりにも難しくて，それの実装を達成するために講師の方の力を借りようと思いました．というのもこのアルゴリズムは公開実装例が２つしか見当たらなかった（しかもどっちも実装を含めて論文になっている）くらいには難解で，ちょっと僕だけではしっかり論文を読めないなと思ったからです．

　プリミティブコースという言葉をパッと出してしまいましたが，今年の L1 コースはプロコトルコースとプリミティブコースの二種類が選択できました．プロトコルコースは暗号化通信ゼミの名前の通り暗号化通信をメインでやる部分です．一方でプリミティブコースは暗号そのものをメインでやる部分です．講師の方々は「コースにとらわれないで流動的であってほしい」と言っていましたが，僕が一にも二にも暗号プリミティブだったこともあって相互で干渉し合うことはあまりできませんでした．ちょこちょこプロトコルコースのボイスチャットにはお邪魔してみてたんですが「プロトコルを実装するってどういうことですか」を質問するレベルでネットワークの知識がなく，まあなんというか多分僕のせいです，すみません．

　それはともかくとして，実は今年は年齢的に最初で最後のチャンスだったのもありなんとしてでも全国大会に通る必要があります．とはいってもセキュリティキャンプに応募してくるような人は強い人が多く，ただ僕が適当に応募課題を書いても通るわけがありません．そこで L1 の応募課題を読んでみると「丁寧であればあるほどよく，さらに分量の制限はない」という旨の記述があったので，僕はとにかく書けることはたくさん書いて絶対に受かると自信をもって言える（逆に言えばこれで受からなかったら自分で納得できる）くらいに内容を仕上げてみました．
　それが功を奏したのが無事選考を通過でき，また講師の先生方にはサーベイ論文と揶揄されて結果的に戦略は成功だったのかなと思います．

　ということで，来年以降の L1 ゼミに応募したい方の参考になればいいなという意味も含め応募課題晒しの文化に則って僕も応募課題をインターネットの海に放り込んでみます．（ちなみに参加期も後で書こうと思っています．技術的な内容は少なめだとは思いますがぜひ読んでみてください！）

Q1

以降の設問文は全て応募課題からの引用です．(プロトコルコースや他ゼミの応募課題も含めた応募課題関連の情報は ここ に色々書いてあります)

以下の語句から一つ選び, その語句に関してできるだけ詳しく説明してください.

  • AES-128-GCM
  • McEliece暗号
  • Grøstl
  • SIDH

SIDH

概要

SIDH は一言で説明すると，楕円曲線の同種写像を利用した耐量子暗号アルゴリズムです．

RSA や DLP といった既存の暗号の基礎問題は比較的簡単に解ける量子アルゴリズムが見つかっており，このまま量子コンピュータの研究が進むと既存の暗号システムが脆弱なものとなってしまいます．そのため耐量子暗号の研究が盛んにおこなわれており，格子ベースのものや符号ベースのものが開発されています．SIDH はそのポスト量子暗号の中で楕円曲線の同種写像グラフを利用したもので，データサイズが小さいことを期待されて研究，開発が進められています．

同種写像問題

SIDH の base problem は，次の同種写像問題に関する仮定となっています [1] ．

base problem
楕円曲線 $E$ と同種写像 $\phi$ による同種な曲線 $E' = \phi(E)$ が与えられたとき，その間にある $\phi$ を求めることは困難である．

SIDH の鍵交換アルゴリズム

同種写像問題を利用した鍵交換をする基本的な手続きは，次の同種関係による可換図式に基づいています．

$$\begin{CD} E @>\phi_B>> E_B\\ @V\phi_A V V @V V\phi_A' V\\ E_A @>\phi_B' >> E_{AB} \end{CD}$$

実際の鍵交換アルゴリズムは次に従います [2]．

public parameter
  • $p = l_A^{e_A}l_B^{e_B} - 1$
  • super singular elliptic curve $E_0(\mathbb{F_{p^2}})$
  • 生成元 $P_A, Q_A \in E\lbrack l_A^{e_A}\rbrack$
  • 生成元 $P_B, Q_B \in E\lbrack l_B^{e_B}\rbrack$
Alice’s key
  • (private) 乱数 $m_A,n_A \in (\Z/l_A^{e_A}\Z)^\times$
  • (private) 同種写像 $\phi_A: E_0 \rightarrow E_A,$　ただし $\ker \phi_A = \left< [m_A]P_A + [n_A]Q_A \right>$
  • (public) $\phi_A(P_B),\ \phi_A(Q_B)$
  • (public) $E_A = \phi_A(E_0)$
Bob’s key
  • (private) 乱数 $m_B, n_B \in (\Z/l_B^{e_B}\Z)^\times$
  • (private) 同種写像 $\phi_B: E_0 \rightarrow E_B,$　ただし $\ker \phi_B = \left< [m_B]P_B + [n_B]Q_B \right>$
  • (public) $\phi_B(P_A),\ \phi_B(Q_A)$
  • (public) $E_B = \phi_B(E_0)$
鍵交換手順

[Alice]

  1. 同種写像 $\phi_A^0: E_B \rightarrow E_{AB}$ を計算．ただし $\ker \phi_A^0 = \left< [m_A]\phi_B(P_A) + [n_A]\phi_B(Q_A) \right>$
  2. $E_{AB} = \phi_A^0(E_B) = \phi_A^0(\phi_B(E_0))$ を計算

[Bob]

  1. 同種写像 $\phi_B^0: E_A \rightarrow E_{AB}$ を計算．ただし $\ker \phi_B^0 = \left< [m_B]\phi_A(P_B) + [n_B]\phi_A(Q_B) \right>$
  2. $E_{AB} = \phi_B^0(E_A) = \phi_B^0(\phi_A(E_0))$ を計算

[shared key]

  • j不変量 $j(E_{AB})$

参考文献

[1] 相川勇輔，“同種写像暗号１：楕円曲線と同種写像グラフ”．https://joint.imi.kyushu-u.ac.jp/wp-content/uploads/2022/08/220802_03aikawa.pdf
[2] David Jao，Luca De Feo，“Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies”

Q1 (発展)

僕は上の問題で SIDH を選択したので次の設問でした．

  1. 似た名前のCSIDHという手法があります. CSIDHとSIDHはどのように異なるのでしょうか.
  2. 「SIDHは解読された」という報告が昨年ありました. 2023年3月時点では更に進化しているようです. 応募時点までで, SIDHの解読手法にはどのようなものがあるのでしょうか.

CSIDH と SIDH の違い

CSIDH は SIDH と同じ超特異楕円曲線の同型類を利用したアルゴリズムですが，SIDH とは異なり計算効率の都合上，基本的には Montgomery曲線のみを使用します (Edwards曲線など他のタイプのものを利用した構成法の研究もされています [1] ) ．

Montgomery曲線は $E:y^2 = x^3+Ax^2 +x$ と表されるもので，後述しますが CSIDH の公開鍵は曲線のみなのでパラメータ $A$ のみとなります．そのため他ポスト量子暗号と比べて公開鍵のサイズが小さいことが利点であった SIDH よりも，さらに公開鍵が小さく [2]，64バイトで十分なセキュリティレベルを確保できます．

$p$ の生成法の違い

SIDH で使用する素数は $p = l_A^{e_A} l_B^{e_B} - 1$ で生成していました．しかし CSIDH では $p = 4l_1 l_2 \cdots l_n - 1$ で生成します [3] ．この $l$ の数が多ければ多いほど，同種写像グラフのパスの数が多くなり強固なアルゴリズムとなります．

鍵の違い

SIDH における秘密鍵は，二種類の乱数とあるカーネルを持つ同種写像でした．また公開鍵は，公開情報の点と曲線を秘密鍵の同種写像で移したものでした． 一方で CSIDH の秘密鍵は ${-m,\cdots,0,\cdots,m}$ からランダムにサンプルされた $n$ 個の整数 $(e_1,\cdots,e_n)$ となります [3] ．ただしこの時の $m$ は，$2m + 1 \geq \sqrt[2n]{p}$ となる最小の $m$ で，$-m$ から $m$ の範囲は非常に小さく $e$ は全体で $(\log p)/2$ ビット程度となります． また CSIDH の公開鍵はモンゴメリ曲線 $E:y^2 = x^3 + Ax^2 + x$ です．この曲線は $A \in \F_p$ のみで特徴づけられるため非常に小さいサイズで表すことができます．

また CSIDH は SIDH と違って曲線上の点を公開情報とする必要がないため，それに対する特殊な攻撃手法を発見するのが難しくなっています．

可換図式の違い

SIDH では単に同種写像を持ってきて鍵交換の可換図式を作っていましたが，CSIDH では群作用による可換図式になります．

$p = 4l_1 l_2 \cdots l_n - 1$ なので $p \equiv 3 \mod 8$ となり，このような超楕円曲線の自己準同型環は，$[n]$ を $n$，Frobenius写像を $\pi = \sqrt{-p}$ に対応させれば $\End(E) \simeq \Z[\pi]$ となります [3] ．そのためこれのイデアル類群 $\cl$ を考えることができ，これは CSIDH の対象となる曲線の同型類の集合 $\ell$ に対して作用し $(\ell, \cl)$ が hard homogenous space [14] になります． 具体的には，$[\a] \in \cl,\ E \in \ell$ として準同型 $\phi_\a(E) = E / \a$ です．ただし $\ker \phi_\a$ は， $\alpha \in \Z[\pi]$ と $\End(E)$ を同一視して $\ker \phi_\a = \bigcap_{\alpha \in \a_s} \ker \alpha$ です．

この群作用で以下の可換図式が作れ，これで鍵交換が行えます．

$$\begin{CD} E @>[\b]>> E_B\\ @V[\a] V V @V V[\a] V\\ E_A @>[\b] >> E_{AB} \end{CD}$$

ただし群作用の計算は，実装としては計算を効率化するために SIDH と同じようにカーネルから同種写像 $\phi_\a$ を生成します． ヒューリスティックではありますが，$\l_i = ([l_i],\pi \mp [1])$ とすれば $[\l_1]\cdots [\l_n]$ のどれか一つ以上が大体 $\cl$ を生成してくれます [3] ．そのため $[\l_1]^{e_1} \cdots [\l_n]^{e_n}$ で $\cl$ の元が表せこれの軌道を考えればよく，$[\l_i]$ による作用のカーネルは捩じれ点 $E[l_i]$ となります．$\#E(\F_p) = p + 1 = 4l_1 l_2 \cdots l_n$ であることから適当な点 $P$ について $\frac{p+1}{l_i} P$ は $l_i$ 等分点となり，Véluの公式から現実的な時間でこの同種写像を計算することができます．

CSIDH の秘密鍵 $(e_1,\cdots,e_n)$ は $\cl$ の元と対応しており，これが各 $[\l_i]$ の肩の指数の部分，つまり作用を適用する回数を表します．また $e_i$ が負の場合は逆の作用となります． この CSIDH のアルゴリズムを同種写像グラフ的に考えれば，カーネルを $E[l_i]$ とする作用 $[\l_i]$ が $n$ 個あって，その $l_i$-isogeny らを秘密鍵 $e_i$ 回適用した結果を公開するものとなります．

SIDH と CSIDH の違いを理解するために CSIDH を実装しました．以下がそのコードになります．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

# csidh.sage
ls = list(prime_range(3, 73))
p = 4 * prod(ls) - 1
Fp = GF(p)
Fp2.<j> =  GF(p^2, modulus=x^2+1)

def montgomery(A):
    return EllipticCurve(Fp2, [0, A, 0, 1, 0])

# 曲線を双有理同値な Montgomery曲線へと変換
def to_montgomery(E):
    Ep = E.change_ring(Fp).short_weierstrass_model()
    a, b = Ep.a4(), Ep.a6()
    P.<x> = PolynomialRing(Fp)
    r = (x^3 + a*x + b).roots()[0][0]
    s = sqrt(3 * r^2 + a)
    if not is_square(s):
        s = -s
    A = 3 * r / s
    return Fp(A)

# 群作用
# [3] "CSIDH: An Efficient Post-Quantum Commutative Group Action"
def group_action(pub, priv):
    E = montgomery(pub)
    es = priv[:]
    
    while any(es):
        x = Fp.random_element()
        P = E.lift_x(x)
        s = 1 if P[1] in Fp else -1
        S = [i for i, e in enumerate(es) if sign(e) == s and e != 0]
        k = prod([ls[i] for i in S])
        Q = ((p + 1) // k) * P
        
        for i in S:
            R = (k // ls[i]) * Q
            if R.is_zero():
                continue
            phi = E.isogeny(R)
            E = phi.codomain()
            Q = phi(Q)
            es[i] -= s
            k //= ls[i]
    return to_montgomery(E)

# e の範囲
m = ceil((sqrt(p) ** (1/len(ls)) - 1) / 2)

# Alice
alice_priv = [randrange(-m, m + 1) for _ in range(len(ls))]
alice_pub = group_action(0, alice_priv)

# Bob
bob_priv = [randrange(-m, m + 1) for _ in range(len(ls))]
bob_pub = group_action(0, bob_priv)

# 鍵交換
shared_alice = group_action(bob_pub, alice_priv)
shared_bob = group_action(alice_pub, bob_priv)

assert shared_alice == shared_bob, "sharing missed"
print("sharing complete", shared_alice)

実行結果

1
2

$ sage csidh.sage
sharing complete 546546252294264083140485008

sharing complete と表示されて，うまく共有できていることが確認できました．

SIDH への攻撃手法と CD attack

SIDH への攻撃手法としては以下のようなものが挙げられます．

Meet-in-the-Middle [4]

一般的に楕円曲線の $l$-isogeny は $l+1$ 個あります．そのため同種写像グラフの各ノードからは $l+1$ 本のエッジが出ています． 同種写像問題で求めたい同種写像の始域と終域に相当するノードから，$l$-isogeny を計算していって同種写像グラフを探索するアルゴリズムが Meet-int-the-Middle です．

$E_0$ と $E_A$ から Alice の $\phi_A$ を求めたいときは，次のようにします．

  1. $E_0$ に全ての $l_A$-isogeny を適用し，得られた曲線を全てメモしておく．
  2. 1 で得られた曲線全てに全ての $l_A$-isogeny を適用しさらにそれをメモする．これを $e_A/2$ 回繰り返す．
  3. 同様に $E_A$ に全ての $l_A$-isogeny を適用し，$E_A$ と $l_A^{e_A / 2}$-同種な曲線をリストアップする．(dual isogeny も $l_A$-isogeny であるため)
  4. 2 と 3 で列挙した曲線のうち等しいものを探し，それぞれの $l_A$-isogeny の適用順から $\phi_A$ を復元する

このアルゴリズムの計算量は $O(l_A^{e_A/2})$ で非常に時間がかかりますが一般的な解法で，また brute force のような素直な方法です．

GPST attack

Alice が同じ秘密鍵を使いまわし，なおかつオラクルとして鍵交換の成功/失敗が得られるとき，evil な Bob が Alice の秘密鍵を復元できてしまうものです．ここでは簡単のため秘密鍵 $m_A,m_B = 1$ として，Alice の秘密鍵 $n_A$ を割り出す方法を説明します [5] ．

本来 Bob は公開鍵として $\phi_B(P_A),\ \phi_B(Q_A),\ E_B = \phi_B(E_0)$ を Alice に渡します．ここで $\phi_B(Q_A)$ を渡す代わりに $[l_A^{e_A - 1}] \phi_B(P_A) + \phi_B(Q_A)$ を渡します． この状態で Alice が通常の鍵共有を行うと，得られる同種写像のカーネルは $\left< \phi_B(P_A) + [n_A] ([l_A^{e_a - 1}] \phi_B(P_A) + \phi_B(Q_A)) \right>$ となります．

$[l_A^{e_a - 1}] \phi_B(P_A)$ は位数が 2 になるはずなので，もしも $n_A$ が偶数であれば $[n_A l_A^{e_a - 1}] \phi_B(P_A) = \O$ となります．逆に $n_A$ が奇数であればカーネルは無限遠点となりません．

よって鍵交換できたか否かのオラクルで $n_A$ の最下位ビットが判別できます．

これを応用すれば最下位ビットに限らず $n_A$ の各ビットを割り出すことができます． $\alpha = (1 + 2^{n-i-1})^{1/2} \mod 2^n$ として，$\phi_B(P_A)$ を公開する代わりに $\alpha (\phi_B(P_A) - 2^{n-i-1} K_i \phi_B(Q_A))$ とします．ただし $K_i$ は $n_A$ の既知に下位ビット分です． またさらに $\phi_B(Q_A)$ を公開する代わりに $\alpha(1 + 2^{n-i-1})\phi_B(Q_A)$ とします．

するとカーネルを構成する点の位数により，$n_A$ の $i$ ビット目が $0$ であれば鍵共有が成立します． よって鍵交換ができたか否かのオラクルで $n_A$ の各ビットが計算できます．

この攻撃により，SIDH ベースの IND-CCA を満たす PKE は作れないと考えられています [5] ．

Torsion-point attack

$l_A^{e_A}$ と $l_B^{e_B}$ の数値のバランスが悪いとき，特に $l_B^{e_B} \geq l_A^{5e_a}$ 程度 [6] の時に多項式時間で攻撃されてしまうようです．

この攻撃は，特に SSI-T で $n$ 人のグループ間鍵共有を行う時に危険になり，例えば $p = l_1^{e_1} l_2^{e_2} \cdots l_n^{e_n} - 1$ として $l_i^{e_i} \simeq l_j^{e_j}$ であるとき，6 人以上の鍵共有なら $A = l_1^{e_1},\ B=l_2^{e_2}\cdots l_n^{e_n}$ とすると $B \geq A^5$ くらいになって攻撃が成立します．

Castryck らによる攻撃

2022年に Castryck と Decru により発見された [7]，Kani の定理を利用した SIKE に対する多項式時間の攻撃法です．このアルゴリズムにより Microsoft の $IKEp217 challenge をシングルコアで 5分以内で解いたり，SIKEp434 や SIKEp751 などのパラメータを現実的な時間で破られています [8] ．また著者による Magma script が公開され [9]，これを基にさらに高速化した実装 [10] もあります．

また Maino らによる Kani の定理を利用した攻撃 [11] も平衡して発見されており，これらを基に Robert によりさらに拡張された攻撃方法 [12] によって一般的な SIDH は破られてしまいました． さらに， Robert の攻撃は $E_0^4 \times E_A^4$ の　8次元の特殊な自己準同型の計算が必要になり，それによって実用に制約がかかる可能性がありますが，2023年に入ってからそれを解決するために SIDH の公開情報をうまく利用した手法 [13] も提案されているようです．

攻撃の原理や仕組みはいまいち理解できませんでした．ただとてもクリティカルなアルゴリズムなのですごく理解したいです．

参考文献

[1] 守谷共起，“同種写像暗号 CSIDH の Edwards 曲線による構成と超特異曲線の信頼できる生成法”
[2] 川合豊，廣政良，相川勇輔，“耐量子計算機暗号 ―量子コンピュータによる解読にも耐え得る次世代暗号―”
[3] Wouter Castryck，Tanja Lange，Chloe Martindale，Lorenz Panny，Joost Renes，“CSIDH: An Efficient Post-Quantum Commutative Group Action”
[4] Brandon Langenberg，“Cryptanalysis of known and attempted attacks on SIDH and SIKE”
[5] Steven D. Galbraith，Christophe Petit，Barak Shani，Yan Bo Ti，“On the Security of Supersingular Isogeny Cryptosystems”
[6] Victoria de Quehen，Péter Kutas，Chris Leonardi，Chloe Martindale，Lorenz Panny，Christophe Petit，Katherine E. Stange，“Improved torsion-point attacks on SIDH variants”
[7] Wouter Castryck，Thomas Decru，“An efficient key recovery attack on SIDH”
[8] Andrew Sutherland，“Castryck-Decru attack on SIKE SIDH (a very rough overview)”
[9] Wouter Castryck，https://homes.esat.kuleuven.be/~wcastryc/
[10] https://github.com/jack4818/Castryck-Decru-SageMath
[11] Luciano Maino，Chloe Martindale，“An attack on SIDH with arbitrary starting curve”
[12] Damien Robert，“Breaking SIDH in polynomial time”
[13] Luciano Maino，Chloe Martindale1，Lorenz Panny，Giacomo Pope，Benjamin Wesolowski，“A Direct Key Recovery Attack on SIDH”
[14] Jean-Marc Couveignes，“Hard Homogeneous”

Q2

Q1で選択した暗号方式を実装してください.

SIDH の実装

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# sidh.sage

# Public Parameters
(la, ea), (lb, eb) = (2, 91), (3, 57)  # $IKEp182
p = la^ea * lb^eb - 1
assert is_prime(p)

Fp2 = GF(p^2)
E = EllipticCurve(Fp2, [1, 0])
Pa, Qa = lb^eb * E.gen(0), lb^eb * E.gen(1)
Pb, Qb = la^ea * E.gen(0), la^ea * E.gen(1)

# Alice
ma = randrange(0, la^ea)
na = randrange(0, la^ea)
phi = E.isogeny(ma * Pa + na * Qa, algorithm="factored")
Ua, Va = phi(Pb), phi(Qb)
Ea = phi.codomain()

# Bob
mb = randrange(0, lb^ea)
nb = randrange(0, lb^ea)
phi = E.isogeny(mb * Pb + nb * Qb, algorithm="factored")
Ub, Vb = phi(Pa), phi(Qa)
Eb = phi.codomain()

# shared key
shared_a = Eb.isogeny(ma * Ub + na * Vb, algorithm="factored").codomain().j_invariant()
shared_b = Ea.isogeny(mb * Ua + nb * Va, algorithm="factored").codomain().j_invariant()

assert shared_a == shared_b, "sharing missed"
print("sharing complete", shared_a)

実行結果

1
2

$ sage sidh.sage
sharing complete 605725309534756129961216154885818743552050541118776976*z2 + 3839126000240784862404930106327311737040660763038229734

sharing complete と表示されてうまく共有できていることが確認できました．

Q2 (発展)

Q2の回答に関して, 「なぜその実装は正しいのですか」と聞かれたとき, あなたならどう返答しますか?

これがすごく難しかったです．Q2 の実装で shared_a と shared_b が等しいこと確認するのではなく，すでにあるパラメータですでにある計算結果と比較してみるべきでした．（講師の先生曰く，その意味では Q2 で $IKEp182 のパラメータを使っているのは良いとのこと）

100回計算してちゃんと鍵共有できてることを確認したのですが，僕自身「これはギャグだろ……」って思ってたのでちゃんとした解答を講師の先生から聞けたのはよかったです．

検証

以下のコードで，Q2 で実装した SIDH のアルゴリズムを 100回計算しました．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# sidh_test.sage
for _ in range(100):
	# ==================================== Q2 implementation ====================================
	# Public Parameters
	(la, ea), (lb, eb) = (2, 91), (3, 57)  # $IKEp182
	p = la^ea * lb^eb - 1
	assert is_prime(p)

	Fp2 = GF(p^2)
	E = EllipticCurve(Fp2, [1, 0])
	Pa, Qa = lb^eb * E.gen(0), lb^eb * E.gen(1)
	Pb, Qb = la^ea * E.gen(0), la^ea * E.gen(1)

	# Alice
	ma = randrange(0, la^ea)
	na = randrange(0, la^ea)
	phi = E.isogeny(ma * Pa + na * Qa, algorithm="factored")
	Ua, Va = phi(Pb), phi(Qb)
	Ea = phi.codomain()

	# Bob
	mb = randrange(0, lb^ea)
	nb = randrange(0, lb^ea)
	phi = E.isogeny(mb * Pb + nb * Qb, algorithm="factored")
	Ub, Vb = phi(Pa), phi(Qa)
	Eb = phi.codomain()

	# shared key
	shared_a = Eb.isogeny(ma * Ub + na * Vb, algorithm="factored").codomain().j_invariant()
	shared_b = Ea.isogeny(mb * Ua + nb * Va, algorithm="factored").codomain().j_invariant()

	assert shared_a == shared_b, "sharing missed"
	print("sharing complete")
	# ===========================================================================================

これを実行すると，一度も 41行目の assert に引っかからず正常終了しました．そのため，Alice と Bob の秘密鍵によって鍵共有が失敗することはないと考えます．

ただ shared の共有ができてアルゴリズムが正しそうでも，電力解析や時間計測系の攻撃のような理論で保障されていない部分に対してもセキュアであるかはわかりません．暗号実装の正しさはそこまで調べなくてはいけませんが，これを判断するのは一人ではとても大変で，また非常に長い時間をかけて精査しなくてはいけません．

そのため，この SIDH の実装に関して「正しい」といえるのは「shared の交換が $IKEp182 のパラメータでできる」というところまでで，これ以上の検証できませんでした．

Q3

あなたが面白いと思った暗号方式を一つ取り上げ, それを説明・実装してください.

非可換群に関連する暗号はどんなものがあるのか気になったので調べてみると braid群を利用した暗号があったため，それについて勉強してみました．

braid群

braid群 $B_n$ は，対称群 $S_n$ の置換の途中で画像のような紐の重なりを考慮した組みひもの集合です [1] ．

この紐の交差の回数に制限がないため，$B_n$ は無限群です．例えば，二本の組み紐があって，その交差の回数を絶対値，最初の交差が左側の紐が上なのか右側の紐が上なのかで符号を対応させれば $B_2 \simeq \Z$ です．

組み紐が等しいというのは，空間上の紐を動かして全く同じ形にできるときを言います．この等号条件により，組み紐という幾何的な表現から，置換と紐の重なりを抽象化して代数的に考えることができるようになります．

演算は対称群と同じように，左側の項による置換操作を行った後に右側の項による置換操作を行うものとなります．逆元としては上下を鏡像反転した組み紐が対応します．

Artin Generator

Artin Generator $\sigma_i\ (0 \leq i < n)$ は，$i$ 番から $i+1$ 番に紐を伸ばしたあと，$i+1$ 番から $i$ 番に紐を伸ばしたものと対応します [1] ．

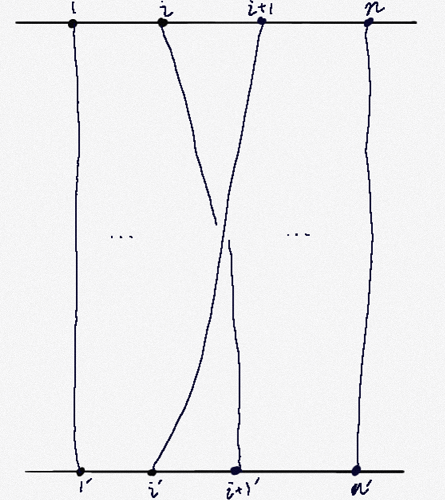
組み紐の演算を想像すれば，次の性質が成り立つことが確かめられます． $$\begin{cases} \sigma _{i} \sigma _{j} =\sigma _{j} \sigma _{i} & \ ( |i-j|>1)\\ \sigma _{i} \sigma _{j} \sigma _{i} =\sigma _{j} \sigma _{i} \sigma _{j} &\ ( |i-j| =1) \end{cases}$$

この Artin Generator $\sigma_1,\sigma_2,\cdots,\sigma_{n-1}$ で braid群を生成することができます [1] ．

上の性質がまさに $B_n$ の基本関係となり，これによって finite presentation が与えられます．

$$B_{n} =\left< \sigma _{1} ,\sigma _{2} ,\cdots ,\sigma _{n-1}\middle| \begin{aligned} \sigma _{i} \sigma _{j} =\sigma _{j} \sigma _{i} & & \ ( |i-j|>1)\\ \sigma _{i} \sigma _{j} \sigma _{i} =\sigma _{j} \sigma _{i} \sigma _{j} & & \ ( |i-j| =1)\end{aligned}\right>$$

数式処理ソフトで braid群を扱うには，例えば自由群を Artin Generator の関係式で剰余をとることなどで使用できます．また sagemath には BraidGroup() というメソッドがあり，これで比較的簡単に計算が行えます．

braid暗号 [2][3]

braid暗号は，braid群 $B_n$ の部分群，$LB_l,RB_r$ によって構成されます．

  • $LB_l$：$B_n$ の紐のうち左側 $l$ 本を用いて構成されるもの
  • $RB_r$：$B_n$ の紐のうち右側 $r$ 本を用いて構成されるもの

定義から $LB_l = (\sigma_1,\sigma_2,\cdots,\sigma_{l-1}),RB_r = (\sigma_{n-r-1}, \sigma_{n-r-2}, \cdots, \sigma_{n-1})$ なので，任意の $a_l \in LB_l, b_r \in RB_r$ に対して $a_l b_r = b_r a_l$ となります．

Base Problem

braid暗号は以下の仮定を基に実現されています．

conjugacy problem
  • 秘密 $a \in LB_l,b \in RB_r$ に対して，$y_1 = axa^{-1},y_2 = bxb^{-1}$ となる $(x,y_1,y_2)$ から秘密 $(a, b)$ を求めるのは計算量的に困難である．

鍵生成

  1. $u \in B_n$ を選択
  2. $a_l \in LB_l$ を選択
  3. $v = a_l u a_l^{-1}$ を計算し，秘密鍵を $a_l$，公開鍵を $(u,v)$ とする

暗号化

メッセージを $m = {0,1}^k$ とし，$H:B_n \rightarrow {0,1}^k$ をハッシュ関数とする．

  1. $b_r \in RB_r$ を選択
  2. $w = b_rub_r^{-1}$ を計算
  3. $d = H(b_rvb_r^{-1}) \oplus m$ を計算し，暗号文を $(w, d)$ とする

複合

以下の式で複合ができます．

$$\begin{aligned} H(a_lwa_l^{-1}) \oplus d &= H(a_lb_rub_r^{-1}a_l^{-1}) \oplus d \ &= H(b_rvb_r^{-1}) \oplus H(b_rvb_r^{-1}) \oplus m \ &= m \end{aligned}$$

実装

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

# braid.sage
import sys
import random
import string
import hashlib
from Crypto.Util.number import *

message = b"Braid cryptosystem"

# H: Bn -> {0,1}^k
# 組み紐の normal form を受け取り，それを文字列とみて sha512 に変換
def hash(b):
	return hashlib.sha512(str(b).encode("utf-8")).digest()

## ------------------
## Key Generation
## ------------------

n = 50		# security parameter
Bn = BraidGroup(n)
gs = Bn.gens()	# Artin Generators

K = 32		# 組み紐の長さが固定になってしまっている

u = random.choices(gs, k=K)	# u の生成

# u \in LB または u \in RB にならないように twist
if not gs[n // 2 - 1] in u:
	u[-1] = gs[n // 2 - 1]
u = prod(u)

# sagemath の left normal form は遅いので right normal form
print(f"u: {prod(u.right_normal_form())}")

al = prod(random.choices(gs[: n//2-2], k=K))	# al の生成
v = al * u * al^-1		# v の生成

# v はすごく長く，出力すると見にくいのでコメントアウト
# print(f"v: {prod(v.right_normal_form())}")

## ------------------
## Encryption
## ------------------

br = prod(random.choices(gs[n//2 + 1 :], k=K))	# br の生成

w = br * u * br^-1
c = br * v * br^-1

h = hash(prod(c.right_normal_form()))

# メッセージを h の長さまでパディング
# パディングがランダムだと複合されたのが確認しにくいため，全て _ でパディングする
pad_length = len(h) - len(message)
left_length = random.randint(0, pad_length)
# pad1 = "".join(random.choices(string.ascii_letters, k=left_length)).encode("utf-8")
# pad2 = "".join(random.choices(string.ascii_letters, k=pad_length-left_length)).encode("utf-8")
pad1 = "".join(random.choices("_", k=left_length)).encode("utf-8")
pad2 = "".join(random.choices("_", k=pad_length-left_length)).encode("utf-8")
message = pad1 + message + pad2

d = []
for i in range(len(h)):
	d.append(chr(message[i] ^^ h[i]))
d = bytes_to_long("".join(d).encode("utf-8"))

# 公開鍵
# print(f"w: {prod(w.right_normal_form())}")	# w も長いので非表示
print(f"d: {d}")

## ------------------
## Decryption
## ------------------

r = al * w * al^-1
r = prod(r.right_normal_form())
r = hash(r)

dd = list(long_to_bytes(d).decode())
xx = []
for i in range(len(r)):
	xx.append(chr(ord(dd[i]) ^^ r[i]))
message = "".join(xx).encode("utf-8")
print(f"message: {message}")

実行結果

1
2
3
4

$ sage braid.sage
u: s0^2*s1*s9*s10*s17*s26*s41*s45*s46*s0*s1*s0*s4*s3*s6*s5*s10*s14*s13*s17*s22*s23*s24*s26*s27*s29*s34*s37*s41*s46*s48
d: 19806161916573509237124676539947687984611237172364598797722173288900842526377722595466863883841047920017790014586600066990583932036270299669472095497855887498686362010501602955605223287447070670055647440631685561699451105007913455296089468
message: b'______Braid cryptosystem________________________________________'

メッセージが暗号化され，また複合もうまく機能していることが確認できました．

参考文献

[1] E. Artin，“Theorie der Zöpfe”
[2] 田中裕子，“ブレイド群を利用した公開鍵暗号系の実装と性能評価実験”
[3] 上村恭子，“Braid 群の conjugacy algorithm について”

Q3 (発展)

また, その暗号が安全かどうかを説明し, 解読手法が存在するなら, それを実装してみてください.

暗号の安全性

braid暗号は，braid群の conjugacy problem の困難性と等価であると考えられており，また conjugacy problem の多項式時間解法はこの暗号が提案された当初は発見されていませんでした [2] ． conjugacy problem は 2018 年の時点でもまだ難しいようです [5] ．

しかし braid群の共役問題全般に関連する非常に強力なツールは古くから知られているようです．Super Summit Set [1] や Ultra Summit Set と呼ばれる集合を列挙する問題に帰着して conjugacy problem を解くアルゴリズムが発見されています [3][4] ．

どちらもある組み紐に対して共役な組み紐をある制限の下で列挙した集合なので，特に Super Summit Set の要素数は，braid群 $B_n$ の組み紐の長さに対して指数関数的に大きくなるため計算するのが大変です．しかし Ultra Summit Set は Super Summit Set にさらに制約を加えたもので，組み紐の長さに対して線形のサイズになる可能性があり，その場合は多項式時間で conjugacy problem が解かれてしまいます [4] ．

しかしこれは完全な多項式時間解法というわけではなく，Ultra Summit Set が十分に大きい場合もあり得るので conjugacy problem の完全な多項式時間解法となったわけではありません [5] ．

他にも同じように Ultra Summit Set のさらに制約を強めた部分集合を定義して，その要素を列挙して conjugacy problem を解こうと研究されているようですが，まだまだ探索空間の上界を多項式で抑えられていないようです [5] ． そのためまだ多項式時間解法が得られておらず，暗号アルゴリズムの基礎問題としては十分に機能します．

しかしうまくいくかわからないとはいえ，これらの conjugacy problem に対する非常に強力なツールが発見されていることは個人的には少し怖いと思う一方，braid群は数学や物理の世界で非常に有用なツールとて詳細に解析されているため，既存の問題に対応さえできればクリティカルに脆弱となる部分が発見されにくいとも考えています．

鍵生成時の $u$ が脆弱な場合の解読手法

braid暗号が多項式時間で解けてしまう場合の例として，鍵生成時の $u$ の選び方が不適切な場合があります [6] ．

$x_1 \in LB_l, x_2 \in RB_r, z \in B_n$ で $$\begin{cases}u=x_{1} x_{2} z & \\ z\ は\ a_{l} ,b_{r} ,x_{1} ,x_{2}\ と可換 &\end{cases}$$ となる $x_1,x_2,z$ が見つかってしまうと脆弱となります．

というのも， $$\begin{aligned}a_{l} wa_{l}^{-1} & =a_{l} b_{r} ub_{r}^{-1} a_{l}^{-1}\\ & =a_{l} b_{r}( x_{1} x_{2} z) b_{r}^{-1} a_{l}^{-1}\\ & =a_{l} b_{r} x_{1} x_{2} b_{r}^{-1} a_{l}^{-1} z\\ & =a_{l} b_{r} x_{1} a_{l}^{-1} x_{2} b_{r}^{-1} z\\ & =\left( a_{l} x_{1} a_{l}^{-1}\right)\left( b_{r} x_{2} b_{r}^{-1}\right) z \end{aligned}$$ となり，ここで

$$\begin{aligned}v & =a_{l} ua_{l}^{-1}\\ & =a_{l}( x_{1} x_{2} z) a_{l}^{-1}\\ & =\left( a_{l} x_{1} a_{l}^{-1}\right) x_{2} z\\ & \\ w & =b_{r} ub_{r}^{-1}\\ & =b_{r}( x_{1} x_{2} z) b_{r}^{-1}\\ & =x_{1}\left( b_{r} x_{2} b_{r}^{-1}\right) z\end{aligned}$$

なので $$\begin{aligned}a_{l} x_{1} a_{l}^{-1} & =vz^{-1} x_{2}^{-1}\\ b_{r} x_{2} b_{r}^{-1} & =x_{1}^{-1} wz^{-1}\end{aligned}$$ となります．

よって $a_lwa_l^{-1} = (vz^{-1}x_2^{-1})(x_1^{-1}wz^{-1})z$ と言う感じで $(v,w,z,x_1,x_2)$ から計算できてしまうため，これを使って $H(a_lwa_l^{-1}) + d$ というように既定の方法で複合できてしまいます．

この攻撃の sagemath による実装は以下のものになります．何度か実行してみると，それなりの確率で攻撃可能な $u$ が生成されてしまうことが確かめられました．

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115

# braid_attack.py
import sys
import random
import string
import hashlib
from Crypto.Util.number import *

message = b"Weak braid cryptosystem"

# H: Bn -> {0,1}^k
# 組み紐の normal form を受け取り，それを文字列とみて sha512 に変換
def hash(b):
	return hashlib.sha512(str(b).encode("utf-8")).digest()

## ------------------
## Key Generation
## ------------------

n = 50		# security parameter
Bn = BraidGroup(n)
gs = Bn.gens()	# Artin Generators

K = 32		# 組み紐の長さが固定になってしまっている

u = random.choices(gs, k=K)	# u の生成

# u \in LB または u \in RB にならないように twist
if not gs[n // 2 - 1] in u:
	u[-1] = gs[n // 2 - 1]
u = prod(u)

# sagemath の left normal form は遅いので right normal form
print(f"u: {prod(u.right_normal_form())}")

al = prod(random.choices(gs[: n//2-2], k=K))	# al の生成
v = al * u * al^-1		# v の生成

# v はすごく長く，出力すると見にくいのでコメントアウト
# print(f"v: {prod(v.right_normal_form())}")

## ------------------
## Encryption
## ------------------

br = prod(random.choices(gs[n//2 + 1 :], k=K))	# br の生成

w = br * u * br^-1
c = br * v * br^-1

h = hash(prod(c.right_normal_form()))

# メッセージを h の長さまでパディング
# パディングがランダムだと複合されたのが確認しにくいため，全て _ でパディングする
pad_length = len(h) - len(message)
left_length = random.randint(0, pad_length)
# pad1 = "".join(random.choices(string.ascii_letters, k=left_length)).encode("utf-8")
# pad2 = "".join(random.choices(string.ascii_letters, k=pad_length-left_length)).encode("utf-8")
pad1 = "".join(random.choices("_", k=left_length)).encode("utf-8")
pad2 = "".join(random.choices("_", k=pad_length-left_length)).encode("utf-8")
message = pad1 + message + pad2

d = []
for i in range(len(h)):
	d.append(chr(message[i] ^^ h[i]))
d = bytes_to_long("".join(d).encode("utf-8"))

# 公開鍵
# print(f"w: {prod(w.right_normal_form())}")	# w も長いので非表示
print(f"d: {d}")

## ------------------
## Attack
## ------------------

# u を分解し，B_n の中心の Artin Generator がどのくらい含まれているか計算
# Tietze() メソッドで Artin Generator による分解ができる
factors = []
for i in u.Tietze():
	factors.append(i - 1)
print(f"factors: {factors}")

x1 = gs[0] / gs[0]
x2 = gs[0] / gs[0]
cnt = 0
for i in factors:
	if i < (n // 2) - 1:
		x1 *= gs[i]
	elif i >= (n // 2) + 1:
		x2 *= gs[i]
	else:
		cnt += 1

# u に B_n の中心の Artin Generator が cnt 個含まれている
# この Artin Generator の左右の Artin Generator が因数に含まれていないと仮定
z = gs[n // 2 - 1]^cnt

if x1 * x2 * z == u:
	print("we can attack")
else:
	print("we cant attack")
	exit(0)

# 攻撃
r1 = v * z^-1 * x2^-1
r2 = x1^-1 * w * z^-1
r = r1 * r2 * z
r = prod(r.right_normal_form())
r = hash(r)

dd = list(long_to_bytes(d).decode())
xx = []
for i in range(len(r)):
	xx.append(chr(ord(dd[i]) ^^ r[i]))
message = "".join(xx).encode("utf-8")
print(f"message: {message}")

実行結果

1
2
3
4
5
6

$ sage braid_attack.sage
u: s18*s6*s13*s18*s39*s42*s41*s4*s3*s6*s13*s14*s13*s15*s18*s17*s22*s24*s30*s29*s34*s33*s35*s34*s36*s35*s39*s38*s41*s45*s48*s47
d: 21772296693486893607149289408660948126947688202738207310405629983816089234225256322774801319789601456755628764147585532520857892920666158747602907879344571304639730721601713491848500596574372321443310046266121413232866464868946691002801110711030587253
factors: [30, 18, 39, 42, 6, 48, 13, 4, 22, 45, 34, 6, 35, 33, 34, 36, 13, 41, 39, 29, 14, 3, 13, 18, 38, 47, 41, 18, 15, 17, 35, 24]
we can attack
message: b'_________________________Weak braid cryptosystem________________'

秘密なしでうまく複合されてしまっていることが確認できました．

この攻撃が発生するケースを考察してみると，$u$ が十分に捩じれていない元を選んでしまった時だと考えられます．例えば $u$ に，$LB_l$ の操作の対象となる組み紐と $RB_r$ の操作の対象となる組み紐の間の内側二本を捩じる元 $\sigma$ が含まれていたとします．またその内側二本を捩じる元の両隣，つまり $LB_l$ を構成する Artin Generator の最大のものと $RB_r$ を構成する Artin Generator の最小のものが $u$ に含まれていなければ $\sigma$ は $u$ の因数全体と可換になるため，$z = \sigma$ として攻撃が成立する可能性が高いと考えます．

単に $u$ をランダムに生成してもなかなかこうはならないとも思えますが，個人的な第一感の $u$ の生成法が脆弱な $u$ を生み出してしまう可能性が高かったため実は結構危ないのではないかとも考えています． その $u$ の悪い生成法は，$B_n$ の Artin Generator から固定の数（例えば 100個）の元を重複ありの順序付きでランダムに得てかけ合わせるというものです．というのも，セキュリティパラメータ $n$ が大きくなると Artin Generator からのサンプリングがスパースになり，$\sigma$ に対応する元が選ばれてもそのすぐ隣の Artin Generator が選ばれる確率が低くなります．またそもそも $\sigma$ に対応する元が選ばれないかもしれません．つまり $u \in LB_l$ または $u \in RB_r$ になってしまい，これは $z = 1$ とすれば同じ攻撃が成り立ちます．これではセキュリティパラメータ $n$ を大きくしたのにむしろ脆弱になってしまいます．

かといって $u$ の生成時の $B_n$ からのサンプリング数を $n$ に対する割合で決めてしまうと，暗号化処理などの計算が非常に重くなってしまいます．というのもそもそも braid群の積の表示は一意でない（例えば sagemath の BraidGroup() は単に掛け算しても一意な表示にならない）場合があります．暗号文の一意性を保つためにもこれを解決しなくてはいけませんが，そのためには，組み紐の left (right) normal form や行列表示を計算しなくてはいけません．しかしこれを計算するアルゴリズムは，組み紐の長さが長ければ長いほど計算に時間がかかってしまいます．

これを防ぐには $u$ の因数に $B_n$ 全体を巡回置換するような元を含めればいいのではないかと考えます．そうすれば上の条件が成り立つ $z$ がないため，この攻撃に対しては安全になると考えます． ただ，巡回置換のような性質の良いもので対処するとまた別の攻撃が考えられてしまいそうな気もします．[5] によると，$\sigma_1 \sigma_2^{-1} \sigma_3 , \sigma_4^{-1}\cdots \sigma_{n-1}^{(-1)^n}$ のような元を利用すれば，十分に捩れるだけでなく Ultra Summit Set も大きくなりよさそうに思えますが，このような元をハードコーディングするのも $u$ をサンプリングする空間が限定的になってしまうため少し不安に感じます． 組み紐の表示の一意性を担保するために長い組み紐が使いにくいことから $n$ をある程度大きくする必要もありますが，そうすると $u \in B_n$ のランダムサンプリングが意外と難しいのではないかと考えています．

参考文献

[1] 上村恭子，“Braid 群の conjugacy algorithm について”
[2] Ki Hyoung Ko，Sang Jin Lee，Jung Hee Cheon，Jae Woo Han，Ju-sung Kang，Choonsik Park，“New Public-key Cryptosystem Using Braid Groups”
[3] V. Gebhardt，“A New Approach to the Conjugacy Problem in Garside Groups”
[4] Chris Gatopoulos，“Braid Group Cryptography”
[5] Maxim Prasolov，“Small braids having a big Ultra Summit Set”
[6] 前田有宏，“ブレイド群を利用した公開鍵暗号系の実装”

Q4

自己アピールできることがあれば, ここに書いてください.

恥ずかしいので非公開です！！！
CTF をやっていたこと，今まで勉強してきた暗号関連の数学のこと（BKZ，Schoof のアルゴリズム，超楕円曲線暗号など），コンパイラやデバッガ，RISC-V 自作の話などブワーーーって書きました．

まとめ

いかかでしたか？（迫真）

ゼミによっては簡潔にまとまっているものを評価するところもあるようなので，僕のこの記事が参考になるかはちょっと微妙です……．
それに僕のこの解答はまだまだ甘い部分が多く僕自身知識が浅いので，もしこの記事を参考に課題を書こうとしている方がいればそれは非推奨です．僕の文章なんかよりもよく纏まった論文はたくさんありますし，講師の先生方は「原著にあたる」気持ちを重要視していたので，言葉通り原著にあたって真に理解してみてください．（暗号界隈はとてもオープンで，ePrint なんかで論文がサッと読めるのはありがたいですね）
これは僕の個人的な意見なのですが，ライブラリやツールに頼るだけでなく中身がどうなっているかを数学としてしっかり理解していくのが暗号の勉強で重要だと感じています．（暗号に限らない話だと思いますが）
またその過程でどんなに時間がかかろうと，最終的に理解して腑に落ちて飲み込めることが一番評価されるポイントだと思っています．他のゼミもそうだとは思いますが，少なくとも L1 ゼミはその部分を評価してくれるような場所だったのでありがたかったです．
ということでもし今応募課題を解こうとして困っている方がいれば，とにかく基本問題だけでもゆっくりと考えて自分の力で思考してみて，暗号を飼うように日々頭の中で理解することを楽しんでみてください．それができれば僕のこの記事なんかよりも自分の理解のために勉強してきた記録が一番の参考文献になっているはずです．さらにそういう方はきっとセキュリティキャンプにも受かると思います．

あとは多分熱意を伝えるのは大事です．講師の先生方を仰天させるような課題をぜひ投稿してみてください！！

つたない文章でしたが読んでいただきありがとうございました．それでは！

comments powered by Disqus
© 2020 - 2023 みつみつみつですか？
Built with Hugo
テーマ Stack は Jimmy によって設計されています。