$$
\gdef\Fp {\mathbb{F} _ p}
\gdef\LB{\mathrm{LB} _ l}
\gdef\RB{\mathrm{RB} _ r}
$$
チーム zer0pts は,今年の 7/15 に zer0pts ctf 2023 を開催しました.
多くの方々に参加していただいて感謝しております.
僕は本コンテストで crypto ジャンルの問題を 4つ作成しました.ここでは作者の想定していた解法を解説していきたいと思います.
[crypto 102pts] easy_factoring (95 solves)
Overview
The word “decomposition” has multiple meanings.
Can you decompose?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
def main():
p = getPrime(128)
q = getPrime(128)
n = p * q
N = pow(p, 2) + pow(q, 2)
print("Let's factoring !")
print("N:", N)
p = int(input("p: "))
q = int(input("q: "))
if isPrime(p) and isPrime(q) and n == p * q:
print(flag)
|
与えられたコードの中で特に重要な部分は上の部分です.
$p,q$ を 128 bits の素数とし,$N := p^2 + q^2$ が与えられます.このとき $p,q$ を発見することができたらフラグを取得できます.
easy_factoring という問題名ですが,やることは素因数分解と見せかけて平方和での分解です.(といっても結局素因数分解が必要になりますが)
Solution
$N$ の平方和での分解は,ガウス整数環 $\mathbb{Z}[i]$ で $N$ の素元分解ができれば解けます.
今 $N$ がガウス素数 $\pi_1,\pi_2,\cdots,\pi_s$ を用いて $N = (\pi_1 \bar \pi_1)(\pi_2 \bar \pi_2)\cdots (\pi_s \bar \pi_s)$ と書けるとします.
このとき $N = a^2 + b^2$ となる $a,b\in \mathbb{Z}$ について,$N = (a + bi)(a - bi) = (\pi_1 \bar \pi_1)(\pi_2 \bar \pi_2)\cdots (\pi_s \bar \pi_s)$ となります.
つまり $N$ を平方和に分解するような整数 $a,b$ は,$a + bi$ として $N$ の $\mathbb{Z}[i]$ での因数に含まれています.
またこれは $N$ を $\mathbb{Z}[i]$ で素元分解してそれらの積の組み合わせを全て計算すれば,その中の少なくとも一つと一致します.
よってこの方法で $p,q$ を復元することができます.
とはいっても $N$ の素元分解に時間がかかる場合があります.そのため何度かサーバに接続して,簡単な $N$ が出るまで繰り返さなくてはいけないことに注意してください.
ソルバどぺ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
from pwn import *
from itertools import combinations
r = process(["python", "server.py"])
r.recvline()
N = ZZ[I](r.recvline()[3:])
print(N)
facs = list(factor(N))
for i in range(len(facs)):
facs[i] = facs[i][0]
print(facs)
prods = []
for i in range(1, len(facs) + 1):
for j in combinations(facs, i):
mul = prod(j)
if is_prime(ZZ(abs(mul[0]))) and is_prime(ZZ(abs(mul[1]))) and mul.norm() == ZZ(N):
print(mul)
r.sendline(str(abs(mul[0])).encode("utf-8"))
r.sendline(str(abs(mul[1])).encode("utf-8"))
r.interactive()
|
実はこんな風に頑張らなくても sagemath に Divisor というメソッドがあるらしく,Divisor(ZZ[I](N)) で $N$ の因数列挙ができるらしいです.
また同じく sagemath に two_squares というメソッドがあり,これを使っても $N$ を平方和に分解できるようです.(これを使う場合は解が一つしか出ないので,たまたま出た解が大きな素数になるまで何度も接続を繰り返す必要があります)
さらにさらに,普通にディオファントス問題としてみて sympy のディオファントス問題ソルバにかけるだでも解けるようです.
easy_factoring は難易度として easy 想定だったので被害は少なかったと思いますが,それでもツールにかけるだけで解けちゃうタイプの非想定解が生まれてしまったのは反省しています.(warmup より solves 多いし)
問題の構想の最初の頃は平方和の分解を使って何らかのシステムに結託攻撃することを考えていたので,そっち方面でもっと練れていたらなという気持ちです.(作問力ぅ……)
[crypto 178pts] Elliptic Ring RSA (27 solves)
Overview
RSA is hard over integer ring.
What about RSA over elliptic curve ring (!?)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
# q.sage
(... omit)
nbits = 8
p = random_prime_bits(nbits)
Fp = GF(p)
a = Fp.random_element()
b = Fp.random_element()
E = EllipticCurve(Fp, [a, b])
ER = EllipticRing(E)
P = ER.encode(flag, 30)
e = 13
C = ER.pow(P, e)
print(f"p: {p}")
print(f"C: {C}")
print(f"a: {a}")
print(f"b: {b}")
print(f"e: {e}")
|
与えられたコードの中で重要な部分は上の部分です.
またこの暗号化処理の上には $\Fp$ を係数として基底を $E(\Fp)$ で張った群環の実装がなされています.(正確に実装するためにそこそこ長いコードになってしまいました)
この問題は,その群環 $\mathrm{ER}$ 上で行われている $e = 13$ の RSA を破ることがゴールとなります.
Solution
群環なので,何らかの多項式環の剰余環と準同型で結べそうな気がしてきます.ということでまずは $E(\Fp)$ の構造とその位数 $o := \#E(\Fp)$ を計算したい気持ちになってきます.
実際に計算すると $o = 192$ であることと,$G := (189, 152)$ によって $E(\Fp) = \left< G \right>$ となることがわかります.
したがって $\mathrm{ER} = \Fp[G]$ となり,$[i]G \mapsto x^i$ とすれば同型 $\Fp[G] \simeq \Fp[x]/(x^o - 1)$ が作れます.
よって $\mathrm{ER}$ 上での RSA は多項式の剰余環での RSA が解ければ破れます.
$o$ の値が小さい(というか $\Fp[x]$ の因数分解がそもそも簡単)なのでこの RSA は簡単に解けます.
$e^{-1}$ の計算は,$x^o - 1$ の各因数 $f _ i$ について $e^{-1} \bmod (p^{\deg {f _ i}} - 1)$ を計算し,最後に CRT でまとめればオッケーです.
ソルバどぺ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
|
import string
import random
class EllipticRingElement:
point = None
def __init__(self, point):
self.point = point
def __add__(self, other):
if self.point == dict():
return other
if other.point == dict():
return self
res = self.point.copy()
for k in other.point.keys():
if k in res:
res[k] += other.point[k]
if res[k] == 0:
res.pop(k)
else:
res[k] = other.point[k]
if res[k] == 0:
res.pop(k)
return EllipticRingElement(res)
def __mul__(self, other):
if self.point == dict() or other.point == dict():
return self.point()
res = dict()
for k1 in other.point.keys():
for k2 in self.point.keys():
E = k1 + k2
k = other.point[k1] * self.point[k2]
if E in res:
res[E] += k
if res[E] == 0:
res.pop(E)
else:
res[E] = k
if res[E] == 0:
res.pop(E)
return EllipticRingElement(res)
def __repr__(self):
st = ""
for k in self.point.keys():
st += f"{self.point[k]}*({k[0]}, {k[1]}) + "
return st[:-3]
class EllipticRing:
E = None
Base = None
def __init__(self, E):
self.E = E
self.Base = E.base()
def __call__(self, pt):
for P in pt:
pt[P] = self.Base(pt[P])
return EllipticRingElement(pt)
def zero(self):
return EllipticRingElement(dict())
def one(self):
return EllipticRingElement({E(0): self.Base(1)})
def pow(self, x, n):
res = self.one()
while n:
if (n & 1):
res = res * x
x = x * x
n >>= 1
return res
def encode(self, m, length):
left = random.randint(0, length)
pad1 = "".join(random.choices(string.ascii_letters, k=left)).encode("utf-8")
pad2 = "".join(random.choices(string.ascii_letters, k=length+len(m)-left)).encode("utf-8")
m = pad1 + m + pad2
Ps = []
while len(Ps) < length:
PP = self.E.random_element()
if PP not in Ps:
Ps.append(PP)
Ps = sorted(Ps)
M = dict()
for coef, pt in zip(m, Ps):
M[pt] = self.Base(coef)
return EllipticRingElement(M)
##################################################################### solve part
with open("output.txt") as f:
p = ZZ(f.readline()[3:])
Fp = GF(p)
C = f.readline()[3:]
a = Fp(f.readline()[3:])
b = Fp(f.readline()[3:])
e = ZZ(f.readline()[3:])
E = EllipticCurve(Fp, [a, b])
ER = EllipticRing(E)
terms = C.split(" + ")
C = dict()
for i in range(len(terms)):
term = terms[i].split("*")
coef = Fp(term[0])
pt = eval(term[1])
x = Fp(pt[0])
y = Fp(pt[1])
if x == 0 and y == 1:
pt = E(0, 1, 0)
else:
pt = E(x, y)
C[pt] = coef
C = ER(C)
o = E.order()
g = E.gens()[0]
print("gens:", E.gens())
print("g: ", g)
print("o: ", o)
print()
rationals = [E(0), g]
for i in range(o - 2):
rationals.append(rationals[-1] + g)
Px.<x> = PolynomialRing(Fp)
def point_to_polynomial(point, rationals):
f = Px(0)
for k in point.keys():
f += point[k] * x^rationals.index(k)
return f
def polynomial_to_point(f, rationals):
d = dict()
cnt = 0
for i in f:
if i != 0:
d[rationals[cnt]] = i
cnt += 1
return ER(d)
f = point_to_polynomial(C.point, rationals)
fi = x^o - 1
factors = list(factor(fi))
for i in range(len(factors)):
factors[i] = factors[i][0]
ms = []
fmods = []
for fmod in factors:
n = fmod.degree()
s = p^n - 1
d = inverse_mod(e, s)
m = pow(f, d, fmod)
ms.append(m)
fmods.append(fmod)
M = crt(ms, fmods)
M = polynomial_to_point(M, rationals)
print("M:", M)
print()
## decode
points = M.point
spoints = sorted(points.items())
for _, coef in spoints:
print(chr(coef), end="")
print()
|
[crypto 226pts] moduhash (16 solves)
Overview
This is related to a base of the theory of elliptic curves!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
CC = ComplexField(256)
for _ in range(100):
n = randint(32, 64)
h1 = to_hash(gen_random_hash(n))
zi = CC.random_element()
print(f"zi : {zi}")
print(f"h1(zi): {hash(zi, h1)}")
h2 = input("your hash> ")
if not hash_eq(h1, h2, CC):
print("your hash is incorrect")
quit()
print(flag)
|
与えられたソースコードの中で重要なのは上の部分です.
$S \colon \mathbb{C} \ni z \mapsto -1/z \in \mathbb{C}$,$T \colon \mathbb{C} \ni z \mapsto z + 1 \in \mathbb{C}$ とします.
また秘匿されたハッシュ関数 $h$ があり,これは $S$ と $T$ のランダムな関数合成によって構成されています.
問題としては,ある $z \in \mathbb{C}$ とそのハッシュによる出力 $h(z)$ が与えられるので $h$ を復元してくださいという問題です.
Solution
まずは $\mathbb{C}$ 全体ではなく,上半平面 $H$ について考えていきましょう.
モジュラー群 $\Gamma := \mathrm{SL}(\mathbb{Z})/\left\lbrace \pm 1 \right\rbrace$ は $H$ に作用します.
この作用による軌道で $H$ を類別できるためその軌道空間 $\Gamma \backslash H$ を考えることができ,そこからうまく代表元を取ってくれば次で定義される基本領域 $F$ と同一視することができます.
$$
F := \left\lbrace \tau \in H \mid |\tau| \geq 1,\ -1/2 < \mathrm{Re}(\tau) \leq 1/2 \right\rbrace
$$
つまり次の命題が成り立ちます.
$$
\forall \tau \in H.\ \exists \gamma \in \Gamma\ s.t.\ \gamma (\tau) \in F.
$$
また後述する $\Gamma$ の生成元から $h \in \Gamma$ なので,$\tau$ と $h(\tau)$ の軌道について $\Gamma \tau = \Gamma h(\tau)$ が成り立ちます.
したがって $\tau, h(\tau) \in H$ が与えられたとき,$\gamma_{\tau}(\tau), \gamma_{h(\tau)}(h(\tau)) \in F$ となる $\gamma_{\tau}, \gamma_{h(\tau)} \in \Gamma$ を見つけることができれば $\gamma_{\tau}(\tau) = \gamma_{h(\tau)}(h(\tau))$ となります.
ここまでくればあとは簡単で,$\gamma_{h(\tau)}^{-1} \circ \gamma_{\tau} = h$ となるため目的のハッシュ関数を計算することができます.
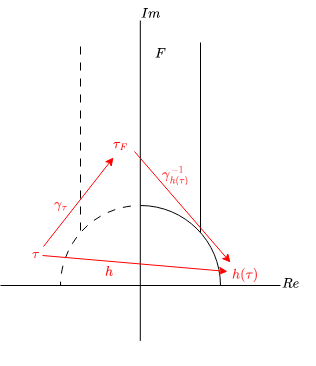
あとは $H$ の元を $F$ に移す $\gamma$ ですが,これは $\Gamma$ のある性質から求めることができます.
$S,T$ を $H$ への作用と見ると
$$
\begin{array}{l}
S=\begin{pmatrix}
0 & -1\\
1 & 0
\end{pmatrix},\
T=\begin{pmatrix}
1 & 1\\
0 & 1
\end{pmatrix}
\end{array}
$$
と表現できます.実は $\Gamma$ は $S,T$ によって生成される,つまり $\Gamma = \left< S, T \right>$ と書けることが知られています.(よって $h \in \Gamma$)
この事実により,$\tau \in H$ が与えられたとき次のアルゴリズムで $F$ に写すことができます.
- $\mathrm{Re}(\tau) > 0.5$ なら $\tau$ に $T^{-1}$ を作用,$\mathrm{Re}(\tau) < -0.5$ なら $\tau$ に $T$ を作用させる
- $|\mathrm{Re}(\tau)| \leq 0.5$ になるまで step 1 を繰り返す(実部を $F$ に合わせる)
- $|\tau| < 1$ のとき $\tau$ に $S$ を作用させる(ノルムを合わせる)
- $\tau \in F$ でなければ step 1 に戻る
ということでこのアルゴリズムを用いれば,上半平面について問題を解くことができます.(ただし $T^{-1} = STSTS$ であることに注意してください)
また下半平面については今までの $H$ の議論を $-H$ に取り替えるだけなので同じ方法で解くことができます.
ソルバどぺ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
|
import math
from pwn import *
def S(z):
return -1/z
def T(z):
return z + 1
def U(z):
return z - 1
def gen_random_hash(n):
r = bytes([getrandbits(8) for _ in range(0, n)])
return r
def to_hash(st):
res = ""
for s in st:
sts = bin(s)[2:].zfill(8)
for x in sts:
if x == "0":
res += "S"
else:
res += "T"
return res
def hash_inv(st):
res = ""
for s in st:
if s == "S":
res = "S" + res
else:
res = "U" + res
res = res.replace("U", "STSTS").replace("SS", "").replace("TSTSTS", "")
return res
def hash(z, h):
res = z
for s in h:
if s == "S":
res = S(res)
elif s == "T":
res = T(res)
elif s == "U":
res = U(res)
else:
exit()
return res
def hash_eq(h1, h2, CC):
for _ in range(100):
zr = CC.random_element()
h1zr = hash(zr, h1)
h2zr = hash(zr, h2)
print(f"abs: {abs(h1zr - h2zr)}")
if abs(h1zr - h2zr) > 1e-15:
return False
return True
def in_fundamental(z):
if -0.5 <= z.real() and z.real() <= 0.5 and abs(z) >= 1:
return True
return False
def gen_to_fundamental_hash(z):
res = ""
while True:
while True:
if z.real() > 0.5:
res += "U"
z = U(z)
elif z.real() < -0.5:
res += "T"
z = T(z)
else:
break
if abs(z) < 1:
res += "S"
z = S(z)
if in_fundamental(z):
break
res = res.replace("U", "STSTS").replace("SS", "").replace("TSTSTS", "")
return res
p = process(["sage", "./server.sage"])
CC = ComplexField(256)
for _ in range(100):
zi = CC(eval(p.recvline().decode("utf-8").strip().split(": ")[1]))
h1zi = CC(eval(p.recvline().decode("utf-8").strip().split(": ")[1]))
p.recvuntil("your hash> ")
print("zi:", zi)
print("h1zi:", h1zi)
hz = gen_to_fundamental_hash(zi)
hh1zi = gen_to_fundamental_hash(h1zi)
hh1zi_inv = hash_inv(hh1zi)
# print("hz:", hz)
# print("hh1zi_inv:", hh1zi_inv)
res = hz + hh1zi_inv
p.sendline(res.encode("utf-8"))
p.interactive()
|
実は元々 moduhash が warmup になる予定でした.
天才 ptr-yudai 氏が SquareRNG を作ってくれていなかったら,今頃僕は責任を取って切腹することになっていたでしょう.
[crypto 340pts] Unlimited Braid Works (6 solves)
Overview
This is probably hard problem.
Is this commutative or non-commutative?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
(...omit)
n = int(input("Input the security parameter> "))
if n < 16:
print("The security parameter is too small !!")
sys.exit(1)
if (n & 1) == 1:
print("The security parameter must be even !!")
sys.exit(1)
print(f"n: {n}")
## ------------------
## Key Generation
## ------------------
Bn = BraidGroup(n)
gs = Bn.gens()
K = 32
u = random.choices(gs, k=K)
# u must be twisted
if not gs[n // 2 - 1] in u:
u[randint(0, K - 1)] = gs[n // 2 - 1]
u = prod(u)
print(f"u: {prod(u.right_normal_form())}")
al = prod(random.choices(gs[: n//2-2], k=K))
v = al * u * al^-1
print(f"v: {prod(v.right_normal_form())}")
## ------------------
## Encryption
## ------------------
pad_length = 64 - len(flag)
left_length = random.randint(0, pad_length)
pad1 = "".join(random.choices(string.ascii_letters, k=left_length)).encode("utf-8")
pad2 = "".join(random.choices(string.ascii_letters, k=pad_length-left_length)).encode("utf-8")
flag = pad1 + flag + pad2
br = prod(random.choices(gs[n//2 + 1 :], k=K))
w = br * u * br^-1
c = br * v * br^-1
h = hash(prod(c.right_normal_form()))
d = []
for i in range(len(h)):
d.append(chr(flag[i] ^^ h[i]))
d = bytes_to_long("".join(d).encode("utf-8"))
print(f"w: {prod(w.right_normal_form())}")
print(f"d: {d}")
|
上のようなコードが与えられます.
これは Braid群を利用した非可換な暗号システムで,Braid群の Conjugacy Problem を基にしています.(問題文の probably hard は conjugacy problem を指している)
$B _ n$ を$n$ 本の組み紐による Braid群とし,そのうち左側 $l$ 本の組み紐の集合を $\LB$,右側 $r$ 本の組み紐の集合を $\RB$ とします.
また $a _ l \in \LB$ を秘密鍵として,公開鍵を $v := a _ l u a _ l^{-1}$ とします.
$m$ をメッセージとし,さらに $H \colon B _ n \to \left\lbrace 0, 1 \right\rbrace^{k}$ をシリアライズ用の関数とします.
このとき暗号化の処理は,ランダムな組み紐 $b _ r \in \RB$ を選び $w := b _ r u b _ r^{-1}$,$d := H(b _ r v b _ r ^{-1}) \oplus$ を計算し,最後に暗号文を $(w, d)$ とするものになっています.
Solution
もし秘密鍵 $a _ l$ がわかっていれば,次のように複合することができます.
$$
\begin{aligned}
H(a_l w a_l^{-1}) \oplus d &= H(a_l b_r u b_r^{-1} a_l^{-1})\\
&= H(b_r v b_r^{-1}) \oplus H(b_r v b_r^{-1}) \oplus m\\
&= m
\end{aligned}
$$
しかし当然 $a _ l$ はわかりません.
この暗号システムは正しく動いているように見えますが,実は $u$ の生成部分に脆弱性があります.
というのも,セキュリティパラメータ $n$ が十分に大きいとき $u$ を構成するための Artin generator がスパースに選ばれます.(ただし $n$ が大きすぎるとサーバ側での暗号化処理に時間がかかりすぎてしまうことに注意してください.問題の解法には全く影響がないため,コンテスト中に alarm(30) を追加して修正しました)
そのため $z$ を $\LB$ と $\RB$ を跨ぐような Artin Generator とすると,$x_1 \in \LB$,$x_2 \in RB$ で次を満たすようなものが存在する確率が非常に高くなります.
$$
\begin{cases}
u = x_1 x_2 z\\
z \text{ is commutive with } a_l,b_r,x_1,x_2
\end{cases}
$$
したがって
$$
\begin{aligned}
v &= a_l u a_l^{-1}\\
&= a_l (x_1 x_2 z) a_l^{-1}\\
&= (a_l x_1 a_l^{-1}) x_2 z
\end{aligned}
$$と
$$
\begin{aligned}
w &= b_r u b_r^{-1}\\
&= b_r (x_1 x_2 z) b_r^{-1}\\
&= x_1 (b_r x_2 b_r^{-1}) z
\end{aligned}
$$
により次の式が得られます.
$$
\begin{aligned}
a_l x_1 a_l^{-1} &= v z^{-1} x_2^{-1}\\
b_r x_2 b_r^{-1} &= x_1^{-1} w z^{-1}
\end{aligned}
$$
よって $a_lwa_l^{-1} = (vz^{-1}x_2^{-1})(x_1^{-1}wz^{-1})z$ とすることで複合することができます.

ソルバどぺ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
|
from pwn import *
import re
import sys
from Crypto.Util.number import long_to_bytes
sys.setrecursionlimit(30000)
def hash(b):
return hashlib.sha512(str(b).encode("utf-8")).digest()
p = process(["sage", "./server.sage"])
p.sendline(b"50")
log.info(p.recvuntil(b": "))
n = int(p.recvline().strip())
log.info(f"n: {n}")
Bn = BraidGroup(n)
gs = Bn.gens()
def braid_eval(x):
res = gs[0] / gs[0]
x = x.split("*")
for i in x:
res *= sage_eval(i, locals={"gs": gs})
return res
log.info(p.recvuntil(b": "))
u = p.recvuntil(b": ")[:-3].strip()
u = re.sub("s([0-9]+)", "gs[\\1]", u.decode())
u = sage_eval(u, locals={"gs": gs})
log.info(f"u: {u}")
v = p.recvuntil(b": ")[:-3].strip()
v = re.sub("\\\\\n", "", v.decode())
v = re.sub("s([0-9]+)", "gs[\\1]", v)
log.info(f"{len(v)}")
v = sage_eval(v, locals={"gs": gs})
log.info(f"v: {v}")
w = p.recvuntil(b": ")[:-3].strip()
w = re.sub("\\\\\n", "", w.decode())
w = re.sub("s([0-9]+)", "gs[\\1]", w)
w = sage_eval(w, locals={"gs": gs})
# log.info(f"w: {w}")
d = int(p.recvline().strip())
log.info(f"d: {d}")
factors = []
for i in u.Tietze():
factors.append(i - 1)
log.info(f"factors: {factors}")
x1 = gs[0] / gs[0]
x2 = gs[0] / gs[0]
cnt = 0
for i in factors:
if i < (n // 2) - 1:
x1 *= gs[i]
elif i >= (n // 2) + 1:
x2 *= gs[i]
else:
cnt += 1
z = gs[n // 2 - 1]^cnt
print(x1)
print(x2)
print(z)
print(x1 * x2 * z == u)
r1 = v * z^-1 * x2^-1
r2 = x1^-1 * w * z^-1
r = r1 * r2 * z
r = prod(r.right_normal_form())
r = hash(r)
dd = list(long_to_bytes(d).decode())
xx = []
for i in range(len(r)):
xx.append(chr(ord(dd[i]) ^^ r[i]))
flag = "".join(xx).encode("utf-8")
log.info(f"flag: {flag}")
p.interactive()
|

