はじめに
超楕円曲線を，こと超楕円曲線暗号のシステムを理解することに絞って最短ルートで解説できたらなと思います．とは言っても，記事の内容に大きな間違いがあるかもしれません．疑問に思ったことや間違っていそうなことがありましたらぜひ twitter なりなんなりで教えてください．僕が悩みます． $\gdef\C{\mathbb{C}} \gdef\R{\mathbb{R}} \gdef\D{\mathcal{D}} \gdef\J{\mathcal{J}} \gdef\F{\mathbb{F} _ p}$
定義とか
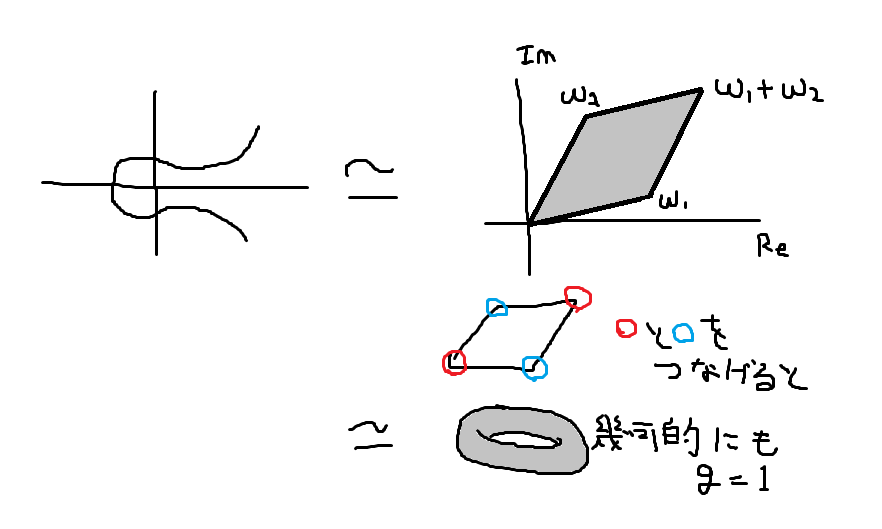
今まで扱ってきた楕円曲線は $v^2 + h(u)v = f(u)$ で $\deg f = 3$ みたいなものでした．これに種数 $g$ という概念を追加します．
曲線の右辺の多項式 $f$ の次数に関して，種数 $g$ を $\deg f = 2g + 1$ となる整数と定義します．
通常の楕円曲線は種数 $1$ の曲線で，またその自然な拡張として $g = 2$ のものや $g = 3$ のものも考えることができるようになります．これらの種数が $1$ よりも大きい代数曲線を超楕円曲線といいます．
定義
体 $K$ を係数とする次数 $2g + 1$ のモニック多項式を $f \in K[u]$ とする．このとき（$K$ 上で定義される）超楕円曲線 $C$ は，次数 $g$ 以下の多項式 $h \in K[u]$ を用いて
$$C: v^2 + h(u)v = f(u)$$
を満たす ${\bar K}^2$ 上の点全体と無限遠点の集合として定義される（正確には射影多様体で考えるべきですがここでは省略します）．
普通超楕円曲線という場合は非特異なものに限りますが，慣用的に特異点を持つ超楕円曲線という言い方をする場合もあります（楕円曲線でもそういうノリはありますよね……気のせい？）．
ちなみに種数の概念が急に出てきて曲線の次数を $2$ ずつ増やしていくのに違和感があるかもしれません．この種数というものは位相幾何の言葉だと「閉曲面の切断によって生じる多様体が連結なままである最大回数」みたいな感じで定義されています．
楕円曲線は $\wp$ 関数のパラメータから生成される格子 $\Lambda$ を使うと $E(\C) \simeq \C / \Lambda$ でした．また $\C/\Lambda$ は幾何学的にはトーラスだったので種数の定義と合致しており，天下り的に見える種数の登場は代数曲線を複素多様体の世界から見たときに自然な導入となるのです．
特異点の条件
曲線ができるだけ非特異な場合を考えたいですが，じゃあ非特異な曲線はどういう曲線なのか気になります．ということで $F = v^2 + h(u)v - f$ としておいて，この関数について調べていきたいと思います．
まず特異点 $P = (x, y)$ では $F(P) = 0$ が成り立ちます．また各変数での偏微分を考えてあげると $$\frac{\partial F}{\partial u} = \frac{d h}{du} v - \frac{df}{du}$$ $$\frac{\partial F}{\partial v} = 2v + h$$ となり，どちらも特異点でゼロになります．よって特異な曲線とは，ある点 $P = (x, y) \in {\bar K}^2$ で $$ \begin{cases} y^2 + h(x)y = f(x) \\ h’(x)y = f’(x) \\ 2y+h(x)=0 \\ \end{cases}$$ となる曲線だということがわかります．
← Singular なネコ（力作）
標準形
うわああああああ $h(u)$ 邪魔すぎて面倒くさい〜〜〜〜．超楕円曲線にも Weierstrass 標準形はないんですか？
$C: v^2 + h(u)v = f(u)$ について $u \rightarrow u,\ v \rightarrow v - h(u) / 2$ と変数変換してあげると
$$\begin{aligned} (v - h(u) / 2)^2 + h(u)(v - h(u) / 2) &= f(u) \\
v^2 - h(u)v + h(u)^2 / 4 + h(u)v - h(u)^2/2 &= f(u) \\
v^2 &= f(u) + h(u)^2 / 2
\end{aligned}$$
となります．また右辺は $\deg h \geq g$ だったので種数も変わりません．
ということでこんな感じで標準形が与えられます．
命題
$K$ 上の超楕円曲線 $C$ について，$\mathrm{char}(K) \neq 2$ であるとき $C$ と双有理同値な $v^2 = f(u)$ 型の種数が同じ超楕円曲線が存在する．
例として $\R$ 上の曲線 $y^2 + (x^2 - 2x - 3)y = 3x^5 - x^4 + x^3 + x^2 - x - 3$ の標準形を求めてみると $y^2 = 3x^5 - x^4 / 2 - x^3 + 5x + 3/2$ となります．
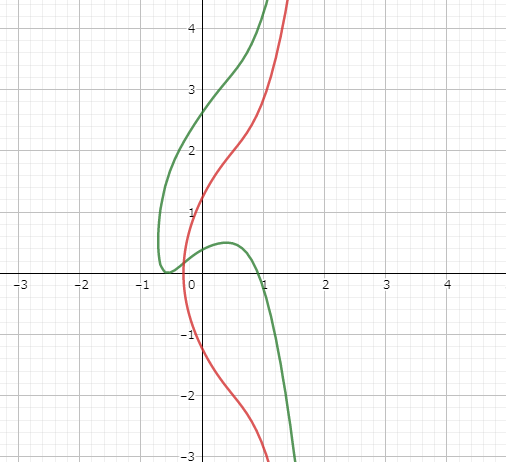← 緑が元の曲線，赤が標準形
曲線上の点
定義
$K$ 上で定義される曲線 $C$ のK-有理点を以下の式で定義する．
$$C(K) = (C \cap K^2) \cup \left\{ P_{\infty} \right\}$$
特に $C = C({\bar K}^2)$．
定義
finite point $P = (x, y)$ について，その反数を $\tilde{P} = (x, -y -h(x))$ とする．無限遠点に関しては $\tilde{P_\infty} = P_\infty$ とする．
また $\tilde{P} = P$ となる点を分岐点と呼び，そうでない点を ordinary point と呼ぶ．
多分この辺は楕円曲線と変わらないと思います．$\tilde{P}$ が曲線上にあることは，次のように代入すれば簡単に確かめられます． $$\begin{aligned} (-y-h(x))^2 + h(x)(-y - h(x)) &= y^2+2h(x)y + h^2(x) - h(x)y - h^2(x)\\ &= y^2 + h(x)y\\ &= f(x) \end{aligned}$$
座標環
多様体上の関数について考えてあげると良いことが起きることが一般的によく知られています．ということで超楕円曲線 $C$ 上の関数を考えてみましょう．
例えば $K$ 上の曲線 $C: F = 0$ 上の関数でぱっと思い浮かぶのは $f \in K[u,v]$ です．ですが $K$ 代数において $C$ は別に代数的じゃないので $f$ の根に $C$ に含まれない点が出てきてしまい，$C$ にぴったりフィットする関数全体として $K[u,v]$ はちょっと大きすぎる気がします．
そこで，じゃあ根が同じくらい $C$ から離れている関数同士は同一視しようという発想が出てきます．数学では結構ありがちですね．ということで Let’s イデアル．
次のような $F$ から生成されるイデアルを考えます．
$$I(C) = \left\{ f \in K[u, v] \mid \forall P \in C , f(P) = 0 \right\}$$
このイデアルで剰余をとってあげた環 $K[u,v] / I(C)$ がちょうど $C$ の関数としてふさわしくなります．$f, g$ が $C$ 上で同じ値をとれば $f \equiv g \mod I(C)$ となっていい感じですね．
このような $C$ 上の代数的な関数全体としてぴったり機能しそうな集合 $K[u, v]/I(C)$ を座標環といいます．
また $I(C) = (F)$ なので，座標環は $K[u,v]/(F)$ とも書けますね．
定義
$K$ 上の超楕円曲線 $C: v^2 + h(u)v = f(u)$ の座標環 $K[C]$ とは次のような剰余環である．
$$K[C] = K[u,v]/(v^2 + h(u)v - f(u))$$
$\bar K$ 上についても同様に $\bar K[C] = \bar K[u,v]/(v^2 + h(u)v - f(u))$ とし，この元を多項式という．
超楕円曲線上の関数 $g \in \bar K [C]$ は，$g$ の $v^2$ を $h(u)v - f(u)$ に置き換えていけば $v$ に関して次数 $1$ になります．つまり $a, b \in \bar K[u]$ を用いて $g = a(u) - b(u)v$ と書くことができます．
$u$ に関して次数 $2g + 1$ 以下，$v$ に関して次数 $1$ 以下で表現できますね．
有理関数
多項式が作れたので有理関数も作りたくなるとことです．有理関数があれば極と零点が定義できますが，実はこれが超楕円曲線を利用した群の構成に密接に関わってくるのです．
定義は簡単かつ自然なのでペッです．
定義
$K$ 上の超楕円曲線 $C$ の関数体 $K(C)$ を以下で定義する．
$$K(C) = \mathrm{Frac}(K[C])$$
$\bar K$ についても同様に $\bar K(C) = \mathrm{Frac}(\bar K[C])$ とし，この元を有理関数という．
また，これから使うことになるので極と零点を定義しておきます．解析っぽい話になってウムウムって感じなので雑にノリで定義します．まあ複素解析とほぼ変わらんのですが．
定義
$f \in K(C)$ とする．$P \in C$ が $f(P) = 0$ を満たす時，$P$ は $f$ の零点であるという．
また，$1 / f(P) = 0$ であるとき $P$ は $f$ の極であるという．
極や零点の位数も定義できます．まあ重複度ですね．$P \in C$ の零点としての位数を $m_Z(P)$，極としての位数を $m_S(P)$ と書きます．
また，有理型関数の有名な命題として以下のようなものがあります．
命題
$f \in K(C)$ について，$f$ の零点全体の集合を $Z_f$，極全体の集合を $S_f$ としたとき以下が成り立つ．
$$\sum_{P \in Z_f} m_Z(P) = \sum_{P \in S_f} m_S(P)$$
要するに重複度を込めて零点と極の数は同じということですね．ほんまか？って思う人もいるかもしれませんが無限遠点パワーです．
曲線上の因子
準備は整いました．さあ，群を作っていきましょう！
楕円曲線では曲線上の点で群をなせましたが，超楕円曲線ではそう簡単にはいきません．
ということで点のタプル的なのを使うんですが，それは以下の感じで定義されます．
定義
$m_1, m_2, \cdots, m_n$ を整数とし，曲線 $C$ 上の有限個の点を $P_1, P_2, \cdots, P_n$ とする．このとき，以下のように表される形式和を曲線 $C$ の因子という．
$$D = \sum_{i=1}^n m_i (P_i)$$
また因子全体の集合を $\D_C$ と書く．
院試がよぎってちょっと嫌ですね……どうでもいいですが $D$ は因子（divisor）の略です．factor とかじゃないので注意です．また点にカッコがついてるのは形式和であることを明示するためです．
実はこの因子全体は，$D_1 = \sum m_i (P_i)$，$D_2 = \sum n_i (P_i)$ の和を $D_1 + D_2 = \sum (m_i + n_i) (P_i)$ とすれば可換群になります．
もしかしたら $D_1$ には含まれているけど $D_2$ には含まれていない点があるかもしれませんが，そういう場合は $D_2$ にも係数 $0$ で含まれているとみなして計算します．
ということで $\D_C$ を作って暗号を作っていこう，という気持ちになるんですがちょっと早計です．というのも $\D_C$ は $C$ に対して大きすぎて性質もよくありません．
まずは因子の次数というのを $\deg D = \sum m_i$ として定義します．こうすれば因子の次数が $0$ である因子同士の和の次数も $\deg (D_1 + D_2) = \sum (m_i + n_i) = 0$ となります．ということで次数 $0$ の因子全体 $\D_C^0$ は $\D_C$ の部分群になりますね．
さらに，次のようにすれば $\D_C^0$ の部分群と $C$ の有理関数を紐付けることできます．
$f \in K(C)$ に対して
$$D_f = \sum_{P \in Z_f} m_Z(P) (P) - \sum_{P \in S_f} m_S(P) (P)$$
を $f$ の主因子といいます．
主因子全体は $\D_C^0$ の部分群になっており，これは零点と極の位数の関係より $D_f \in \D_C^0$ であることと，$f, g \in K(C)$ について $D_f + D_g = D_{fg}$ であることから確かめられます．
この主因子を使えば，名前はよく聞くけどよくわからない積分で出てきそうなアレが定義できるようになります！！！
定義
超楕円曲線 $C$ のゼロ因子群を $\D^0$，主因子群を $\D^l$ とする時
$$\J_C = \D^0 / \D^l$$
を曲線のヤコビアンという．
名前はヤコビアンですが，積分の変数変換のヤコビアンとは違うものなので注意です．こいつは本質的には多様体です．ﾓｼﾞｭ…ﾓｼﾞｭ……
これは $\D^l$ による剰余類群なので $D_1, D_2 \in \D^0$ が $D_1 - D_2 \in \D^l$ を満たす時 $D_1 \equiv D_2 \mod \D^l$ ということです．
ヤコビアンでの演算は，まあ適当に代表元同士で計算してその剰余類を計算すればいいんじゃないでしょうか．
ちなみに通常の楕円曲線では，このヤコビアンの元と曲線上の点が一対一対応します．超楕円曲線での群演算が楕円曲線での群演算の拡張になっていて嬉しいですね．
まず $D = \sum m_i (P_i) \in \D^0$ に対して $Q = \sum m_i P_i$ と置けば，$D - (Q) + (P_\infty)$ が実は主因子となり $D \equiv (Q) - (P_\infty) \mod D^l$ となります．
また一対一であることについては，異なる点 $P_1, P_2 \in C$ について $(P_1) - (P_\infty) \equiv (P_2) - (P_\infty)$ であることから $(P_1) - (P_2) \equiv 0$ となってしまい，$(P_1) - (P_2) \in \D^l$ となって矛盾します．
ということで $D \mapsto Q$ と対応させれば同型が成り立ちます．
Mumford 表現
ヤコビアン $\J_C$ は因子類群として定義できましたが，因子は複数個の点と係数の組として扱わなくてはいけないのでちょっと複雑です．
実は因子の剰余類を簡潔に表現するために，$\J_C$ の元を２つの多項式で表現する天才的な発明があります．これを Mumford表現といいます．
Mumford表現では Harley加算などの高速な加算アルゴリズムも見つかり，計算機的にも嬉しいことが多いのです．
ということで Mumford表現を説明したいところですが，実はこれは一般の因子に対しては定義されません．じゃあどうするか，次のような因子を考えます．
定義
有限個の点 $P_1, P_2, \cdots, P_n$ と無限遠点により定義された因子 $D$ が次の条件を満たす時，$D$ は半被約因子であるという．
- $D = \sum_{i = 1}^n m_i (P_i) - (\sum_{i = 1}^n m_i) (P_\infty)\ \ (m_i > 0)$
- $P_i \neq \tilde P_i$ ならば $i$ と異なるすべての $j$ について $P_j \neq \tilde P_i$
- $P_i$ が分岐点ならば $m_i = 1$
つまり半被約因子とは，$\D^0$ に含まれる，無限遠点以外の係数が全て正で $\tilde P$ も持たず分岐点も複数持たないような因子です．
例えば $\mathbb{F} _ 3$ 上の超楕円曲線 $C: y^2 = x^5 + 2x^3 + 1$ について考えていきましょう．$x^2 + 2x + 2$ の根を $\alpha$ として $P_1 = (0, 1),\ P_2 = (0, 2),\ P_3 = (\alpha, 0) \in C$ とします．
この時，適当な因子を選んで半被約因子であるか判定した結果は次のようになります（実は過去に yoshiking さんがひよこ判定士の如くやってくれました）．
- $2(P_1) + (P_3) - 3(P_\infty)$ はオーケー
- $2(P_1) - (P_3) - (P_\infty)$ はダメ (条件1)
- $2(P_1) + (P_3) - 2(P_\infty)$ はダメ (条件1)
- $(P_2) + (P_3) - 2(P_\infty)$ はオーケー
- $(P_1)+(P_2)-2(P_\infty)$ はダメ (条件2)
- $2(P_3) - 2(P_\infty)$ はダメ (条件3)
こんな感じで半被約因子が定義できますが，ちょっと恣意的な感じがしますね．実は任意の因子はそれと $\D^l$ の下で等しい半被約因子を持つことが知られているのです！
つまり $\J_C$ 内の剰余類の代表現として半被約因子をとってくることができます．Mumford表現は半被約因子という特別な因子でしか定義できませんが，$\J_C$ の表現としては十分機能することがわかりますね．
定義
体 $K$ 上の超楕円曲線 $C: F= 0$ における半被約因子 $D = \sum m_i (P_i) - (\sum m_i)(P_\infty)$ の Mumford表現とは，$U, V \in \bar K[X]$ の組 $(U, V)$ のことである．ただし $U, V$ は $P_i = (x_i,y_i),\ U_i = X - x_i$ とおいた時以下の式を満たすものである．
$$\begin{cases}
U=\prod _ {i=1}^{n} U_{i}^{m_{i}} & \\
F-V^{2} \equiv 0\bmod U & \\
\deg U >\deg V &
\end{cases}$$
受け取った因子の Mumford表現を計算するアルゴリズムはちょっと複雑です（もしかしたらこのアルゴリズム単体で記事を書くかもしれません）．
みんな sagemath 使おう．ヤコビアンの元の表現を，点の組の表現か Mumford表現か選べます．
被約因子
実は半被約因子は暗号として使うのに少々問題があります．というのも半被約因子による表現は $\J_C$ の元の一意な表現とはなりません．つまり平文と暗号文の間に一対一対応が作れなくなるしハッシュ化も大変です．
これを解決するものとして，以下のような因子が考えられています．
定義
種数 $g$ の超楕円曲線の半被約因子 $(U, V)$ について，特に $\deg U \leq g$ であるものを被約因子という．
まあ定義は簡単ですがほえ〜んって感じじゃないでしょうか．
実は被約因子は $\D^l$ の下でそれと同値な被約因子が一意に存在します．またこれをアルゴリズム的に構成することも可能です（これも単体で記事書くかも．期待はしないでね）．
ですので，$\J_C$ の元の表現は半被約因子ではなく，被約因子の Mumford表現にすると色々と嬉しくなります．ちなみに sagemath は被約因子を使ってくれます．みんな sagemath 使おう．
$\J_C$ の有限部分群
実は今のヤコビアンのままでは超楕円曲線暗号を楕円曲線暗号のように ElGamal のシステムに乗せるのは無理です．というのも一般に $\bar K$（特に $\bar{\mathbb{F} _ p}$）は無限位数なのでヤコビアンも無限位数になってしまうのです．ElGamal のシステムに乗せるには，少なくとも有限群でなくてはいけません．
ということで $\J_C$ の有限部分群を考えていきましょう．と言ってもこれは簡単です．
とりあえず今のヤコビアンが Mumford表現を使ってどう表現されるのか明示しておきます． $$\J_C = \left\{ (U, V) \in \bar K[X]^2 \mid \deg V < \deg U < g,\ F - V^2 \equiv 0 \mod U \right\}$$
これの $K$-有理点のようなものを考えれば良くて，次のようにします．
$$\J_C(K) = \left\{ (U, V) \in K[X]^2 \mid (U, V) \in \J_C \right\}$$
$K$ が有限であれば $U, V$ の次数が制限されるので自然に $\J_C(K)$ も有限位数となります．暗号として実装する場合は $K = \mathbb{F} _ p$ として $\J_C(\mathbb{F} _ p)$ を計算するのが一番自然かと思います．
上では Mumford表現を使って $K$-有理点を構成しましたが，標数 $p$ の有理点は因子による表現でもかなり簡潔に表記できます．Frobenius写像 $\varphi$ を
$$\varphi: \J_C \ni D \longmapsto D^p \in \J_C$$
と定めます．ここで注意なのが，$D^p = \sum m_i (P_i)^p - (\sum m_i)(P_\infty),\ P^p = (x^p, y^p)$ です．
この Frobenius写像により固定される集合こそが $\mathbb{F} _ p$-有理点 $\J_C(\mathbb{F} _ p) = \left\{ D \in \J_C \mid \varphi(D) = D \right\}$ となります（そもそも $K$-有理点という概念が $G_{\bar K / K}$ で固定される集合なので）．
超楕円曲線暗号
やっとこさ暗号のシステムの話になります．といってもここまで理解できてればあとは簡単で，超楕円曲線暗号は $C$ のヤコビアン $\J_C(\F)$ での離散対数問題に関する暗号です．
公開パラメータ
$p$: 素数
$C$: $\F$ 上の超楕円曲線
鍵生成
$D_g$: ランダムな $\J_C(\F)$ の元
$s$: ランダムな $\left\{0,\cdots,\# \J_C(\F) \right\}$ の元
$D = sD_g$ を計算し，$(D, D_g)$ を公開鍵，$s$ を秘密鍵とする．
暗号化
$M \in C$ を平文として $r \in \left\{0, \cdots, \# \J_C(\F) \right\}$ を乱数とする．
$$(C_1, C_2) = (rD_g,\ rD + M)$$
複合
$$\begin{aligned}
C_2 - sC_1 &= rD + M - srD_g
&= srD_g + M - srD_g
&= M
\end{aligned}$$
sagemath で実装する場合は，HyperEllipticCurve(f, h) で超楕円曲線を生成し，C.jacobian() でヤコビアンを生成，J(GF(p)) で $\F$-有理点を作ってやりましょう．
僕も実装してみた．かなりガバいのでこの実装は全人類真似しないでください．
|
|
それでは良き超楕円曲線ライフを！
ちなみに超楕円曲線暗号は安全な曲線の生成法や計算量に問題があり，まだ研究段階です……なんもかんもヤコビアンの位数計算が悪い（気がする）