$$
\gdef\Fp {\mathbb{F} _ p}
\gdef\LB{\mathrm{LB} _ l}
\gdef\RB{\mathrm{RB} _ r}
$$
Team zer0pts held zer0pts ctf 2023 on July 15.
I’m happy to see so meny people participating!
I created 4 challenges in the crypto genre for this contest. Here, I’d like to explain the intended solution for me.
[crypto 102pts] easy_factoring (95 solves)
Overview
The word “decomposition” has multiple meanings.
Can you decompose?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
def main():
p = getPrime(128)
q = getPrime(128)
n = p * q
N = pow(p, 2) + pow(q, 2)
print("Let's factoring !")
print("N:", N)
p = int(input("p: "))
q = int(input("q: "))
if isPrime(p) and isPrime(q) and n == p * q:
print(flag)
|
The most important part of the given code is above.
Let $p,q$ are large prime and $N := p^2 + q^2$. Given $N$, we need restore $p,q$ from $N$ to get the flag.
The name of the challenge is easy_factoring, but what it is supposed to be is a sum-of-squares decomposition disguised as prime factorization. (Although, in the end, prime factorization is required)
Solution
The decomposition of $N$ into sums of squares can be solved if the Gaussian integer ring $\mathbb{Z}[i]$ can be solved for the prime elements of $N$.
Now, $N$ is expressed as $N = (\pi_1 \bar \pi_1)(\pi_2 \bar \pi_2) \cdots (\pi_s \bar \pi_s)$ by Gaussian primes $\pi_1,\pi_2,\cdots,\pi_s$.
Then for $a,b \in \mathbb{Z}$ such that $N = a^2 + b^2$, $N = (a + bi)(a - bi) = (\pi_1 \bar \pi_1)(\pi_2 \bar \pi_2) \cdots (\pi_s \bar \pi_s)$ holds.
In short, integers $a,b$ such that $N$ decomposes into a sum of squares are included in the factors in $\mathbb{Z}[i]$ of $N$ as $a + bi$.
Also, if you compute all combinations of the products of the factors of N in $\mathbb{Z}[i]$, it is coincide with at least one of them.
Therefore we can recover $p,q$ by this method.
But, factoring $N$ may take a long time. Note that we have to connect to the server several times until we get a easy $N$.
Solver is here.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
from pwn import *
from itertools import combinations
r = process(["python", "server.py"])
r.recvline()
N = ZZ[I](r.recvline()[3:])
print(N)
facs = list(factor(N))
for i in range(len(facs)):
facs[i] = facs[i][0]
print(facs)
prods = []
for i in range(1, len(facs) + 1):
for j in combinations(facs, i):
mul = prod(j)
if is_prime(ZZ(abs(mul[0]))) and is_prime(ZZ(abs(mul[1]))) and mul.norm() == ZZ(N):
print(mul)
r.sendline(str(abs(mul[0])).encode("utf-8"))
r.sendline(str(abs(mul[1])).encode("utf-8"))
r.interactive()
|
Actually, sagemath has a method Divisor, which can be used to enumerate the factors of $N$ using Divisor(ZZ[I](N)).
Also sagemath has a method two_squares, which can be used to decompose $N$ into sum of square.
Furthermore, it seems that the Diophantine problem can be solved by simply applying the Diophantine problem solver in sympy.
I think easy_factoring was assumed to be easy in terms of difficulty, so there was little damage. But I regret that a non-intended solution was created that could be solved by just applying the tool.
At the beginning of the problem design, I was thinking of using the decomposition of the sum of squares to do collution attack with some system.
I wish I could have been more creative in that area. (I lacked the ability to create challenge…)
[crypto 178pts] Elliptic Ring RSA (27 solves)
Overview
RSA is hard over integer ring.
What about RSA over elliptic curve ring (!?)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
# q.sage
(... omit)
nbits = 8
p = random_prime_bits(nbits)
Fp = GF(p)
a = Fp.random_element()
b = Fp.random_element()
E = EllipticCurve(Fp, [a, b])
ER = EllipticRing(E)
P = ER.encode(flag, 30)
e = 13
C = ER.pow(P, e)
print(f"p: {p}")
print(f"C: {C}")
print(f"a: {a}")
print(f"b: {b}")
print(f"e: {e}")
|
The most important part of the given code is above.
Given a group ring constructed by coefficients $\mathbb{F}_p$ and basis $E(\mathbb{F}_p)$. (Sorry, the source code is complex to implement properly)
The task is to break the RSA on this group ring $\mathrm{ER}$.
Solution
Since it is a group ring, it seems to be homomorphic to the residue ring of some polynomial ring.
So, first of all, I feel like computing the structure of $E(\Fp)$ and its order $o := \#E(\Fp)$.
Actually, the calculation shows that $o = 192$ and $E(\Fp) = \left< G \right>$ by $G := (189, 152)$.
Hence $\mathrm{ER} = \Fp[G]$, and if $[i]G \mapsto x^i$ then we can construct the isomorphism $\Fp[G] \simeq \Fp[x]/(x^o - 1)$.
Therefore, RSA on $\mathrm{ER}$ can be broken if RSA on the residue ring can be solved.
This is easy because the $o$ is small (or rather, it is generally known that the factorization of $\Fp[x]$ is easy).
To compute e-1, just compute e-1 mod (pdegfi-1) for each factor fi of xo-1, and finally sum it up with CRT.
To compute $e^{-1}$, just compute $e^{-1} \bmod (p^{\deg f_i})$ for each factor $f_i$ of $x^o - 1$, and finally combine by CRT.
Solver is here.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
|
import string
import random
class EllipticRingElement:
point = None
def __init__(self, point):
self.point = point
def __add__(self, other):
if self.point == dict():
return other
if other.point == dict():
return self
res = self.point.copy()
for k in other.point.keys():
if k in res:
res[k] += other.point[k]
if res[k] == 0:
res.pop(k)
else:
res[k] = other.point[k]
if res[k] == 0:
res.pop(k)
return EllipticRingElement(res)
def __mul__(self, other):
if self.point == dict() or other.point == dict():
return self.point()
res = dict()
for k1 in other.point.keys():
for k2 in self.point.keys():
E = k1 + k2
k = other.point[k1] * self.point[k2]
if E in res:
res[E] += k
if res[E] == 0:
res.pop(E)
else:
res[E] = k
if res[E] == 0:
res.pop(E)
return EllipticRingElement(res)
def __repr__(self):
st = ""
for k in self.point.keys():
st += f"{self.point[k]}*({k[0]}, {k[1]}) + "
return st[:-3]
class EllipticRing:
E = None
Base = None
def __init__(self, E):
self.E = E
self.Base = E.base()
def __call__(self, pt):
for P in pt:
pt[P] = self.Base(pt[P])
return EllipticRingElement(pt)
def zero(self):
return EllipticRingElement(dict())
def one(self):
return EllipticRingElement({E(0): self.Base(1)})
def pow(self, x, n):
res = self.one()
while n:
if (n & 1):
res = res * x
x = x * x
n >>= 1
return res
def encode(self, m, length):
left = random.randint(0, length)
pad1 = "".join(random.choices(string.ascii_letters, k=left)).encode("utf-8")
pad2 = "".join(random.choices(string.ascii_letters, k=length+len(m)-left)).encode("utf-8")
m = pad1 + m + pad2
Ps = []
while len(Ps) < length:
PP = self.E.random_element()
if PP not in Ps:
Ps.append(PP)
Ps = sorted(Ps)
M = dict()
for coef, pt in zip(m, Ps):
M[pt] = self.Base(coef)
return EllipticRingElement(M)
##################################################################### solve part
with open("output.txt") as f:
p = ZZ(f.readline()[3:])
Fp = GF(p)
C = f.readline()[3:]
a = Fp(f.readline()[3:])
b = Fp(f.readline()[3:])
e = ZZ(f.readline()[3:])
E = EllipticCurve(Fp, [a, b])
ER = EllipticRing(E)
terms = C.split(" + ")
C = dict()
for i in range(len(terms)):
term = terms[i].split("*")
coef = Fp(term[0])
pt = eval(term[1])
x = Fp(pt[0])
y = Fp(pt[1])
if x == 0 and y == 1:
pt = E(0, 1, 0)
else:
pt = E(x, y)
C[pt] = coef
C = ER(C)
o = E.order()
g = E.gens()[0]
print("gens:", E.gens())
print("g: ", g)
print("o: ", o)
print()
rationals = [E(0), g]
for i in range(o - 2):
rationals.append(rationals[-1] + g)
Px.<x> = PolynomialRing(Fp)
def point_to_polynomial(point, rationals):
f = Px(0)
for k in point.keys():
f += point[k] * x^rationals.index(k)
return f
def polynomial_to_point(f, rationals):
d = dict()
cnt = 0
for i in f:
if i != 0:
d[rationals[cnt]] = i
cnt += 1
return ER(d)
f = point_to_polynomial(C.point, rationals)
fi = x^o - 1
factors = list(factor(fi))
for i in range(len(factors)):
factors[i] = factors[i][0]
ms = []
fmods = []
for fmod in factors:
n = fmod.degree()
s = p^n - 1
d = inverse_mod(e, s)
m = pow(f, d, fmod)
ms.append(m)
fmods.append(fmod)
M = crt(ms, fmods)
M = polynomial_to_point(M, rationals)
print("M:", M)
print()
## decode
points = M.point
spoints = sorted(points.items())
for _, coef in spoints:
print(chr(coef), end="")
print()
|
[crypto 226pts] moduhash (16 solves)
Overview
This is related to a base of the theory of elliptic curves!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
CC = ComplexField(256)
for _ in range(100):
n = randint(32, 64)
h1 = to_hash(gen_random_hash(n))
zi = CC.random_element()
print(f"zi : {zi}")
print(f"h1(zi): {hash(zi, h1)}")
h2 = input("your hash> ")
if not hash_eq(h1, h2, CC):
print("your hash is incorrect")
quit()
print(flag)
|
The most important part of the given code is above.
Let $S \colon \mathbb{C} \ni z \mapsto -1/z \in \mathbb{C}$ and $T \colon \mathbb{C} \ni z \mapsto z + 1 \in \mathbb{C}$ be the maps.
There is also a secret hash function $h$, which consists of random composition of $S$ and $T$.
This challenge is to recover $h$ given some $z \in \mathbb{C}$ and its hash $h(z)$.
Solution
At first, consider the upper half-plane $H$ instead of the entire $\mathbb{C}$.
Modular group $\Gamma := \mathrm{SL}(\mathbb{Z})/\left\lbrace \pm 1 \right\rbrace$ is a group action of $H$.
Since $H$ can be classified by orbits due to this action, so we can consider its orbit space $\Gamma \backslash H$. And, if the representatives are picked properly, this can be identify with fundamental domain $F$ defined below.
$$
F := \left\lbrace \tau \in H \mid |\tau| \geq 1,\ -1/2 < \mathrm{Re}(\tau) \leq 1/2 \right\rbrace
$$
In other words, the following proposition holds.
$$
\forall \tau \in H.\ \exists \gamma \in \Gamma\ s.t.\ \gamma (\tau) \in F.
$$
Also, since $h \in \Gamma$ (for the property of $\Gamma$ described later),$\Gamma \tau = \Gamma h(\tau)$ is holds for the orbit $\tau$ and $h(\tau)$.
Thereore, given $\tau, h(\tau) \in H$, $\gamma_{\tau}(\tau) = \gamma_{h(\tau)}(h(\tau))$ holds for $\gamma_{\tau}, \gamma_{h(\tau)} \in \Gamma$ such that $\gamma_{\tau}(\tau), \gamma_{h(\tau)}(h(\tau)) \in F$.
Finally, the hash $h$ can be computed by $\gamma_{h(\tau)}^{-1} \circ \gamma_{\tau} = h$.
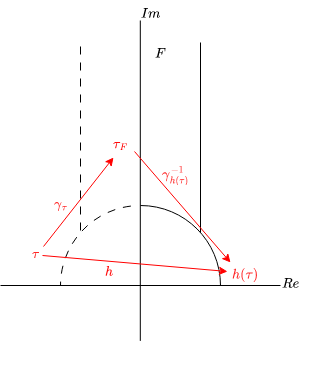
For compute $\gamma$ such that a element of $H$ maps into $F$, some property of $\Gamma$ can be used.
Viewing $S,T$ as an action of modular group on $H$, these are represented by the following matrices.
$$
\begin{array}{l}
S=\begin{pmatrix}
0 & -1\\
1 & 0
\end{pmatrix},\
T=\begin{pmatrix}
1 & 1\\
0 & 1
\end{pmatrix}
\end{array}
$$
Actually, $\Gamma$ is generated by $S$ and $T$. (Therefor, $h \in \Gamma$ holds)
By this fact, given $\tau \in H$, $\tau$ maps to $F$ by the following algorithm.
- If $\mathrm{Re}(\tau) > 0.5$ then action $T^{-1}$ to $\tau$, else if $\mathrm{Re}(\tau) < -0.5$ then action $T$ to $\tau$.
- Repeat step 1 until $|\mathrm{Re}(\tau)| \leq 0.5$ is true. (To align the real part of $\tau$ with $F$).
- If $|\tau| < 1$ then action $S$ to $\tau$. (To expand the norm of $\tau$ to fit $F$).
- If $\tau \in F$ is false, back to step 1.
So, using above algorithm, this challenge can be solved for the upper half-plane. (Note that $T^{-1} = STSTS$).
The lower half-plane can be solved in the same way by simply replacing $H$ with $-H$.
Solver is here.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
|
z + 1
def U(z):
return z - 1
def gen_random_hash(n):
r = bytes([getrandbits(8) for _ in range(0, n)])
return r
def to_hash(st):
res = ""
for s in st:
sts = bin(s)[2:].zfill(8)
for x in sts:
if x == "0":
res += "S"
else:
res += "T"
return res
def hash_inv(st):
res = ""
for s in st:
if s == "S":
res = "S" + res
else:
res = "U" + res
res = res.replace("U", "STSTS").replace("SS", "").replace("TSTSTS", "")
return res
def hash(z, h):
res = z
for s in h:
if s == "S":
res = S(res)
elif s == "T":
res = T(res)
elif s == "U":
res = U(res)
else:
exit()
return res
def hash_eq(h1, h2, CC):
for _ in range(100):
zr = CC.random_element()
h1zr = hash(zr, h1)
h2zr = hash(zr, h2)
print(f"abs: {abs(h1zr - h2zr)}")
if abs(h1zr - h2zr) > 1e-15:
return False
return True
def in_fundamental(z):
if -0.5 <= z.real() and z.real() <= 0.5 and abs(z) >= 1:
return True
return False
def gen_to_fundamental_hash(z):
res = ""
while True:
while True:
if z.real() > 0.5:
res += "U"
z = U(z)
elif z.real() < -0.5:
res += "T"
z = T(z)
else:
break
if abs(z) < 1:
res += "S"
z = S(z)
if in_fundamental(z):
break
res = res.replace("U", "STSTS").replace("SS", "").replace("TSTSTS", "")
return res
p = process(["sage", "./server.sage"])
CC = ComplexField(256)
for _ in range(100):
zi = CC(eval(p.recvline().decode("utf-8").strip().split(": ")[1]))
h1zi = CC(eval(p.recvline().decode("utf-8").strip().split(": ")[1]))
p.recvuntil("your hash> ")
print("zi:", zi)
print("h1zi:", h1zi)
hz = gen_to_fundamental_hash(zi)
hh1zi = gen_to_fundamental_hash(h1zi)
hh1zi_inv = hash_inv(hh1zi)
# print("hz:", hz)
# print("hh1zi_inv:", hh1zi_inv)
res = hz + hh1zi_inv
p.sendline(res.encode("utf-8"))
p.interactive()
|
Actually, I had planned to use moduhash as a crypto warmup.
If genius ptr-yudai had not created SquareRNG, I would have committed Seppuku (ritual suicide).
[crypto 340pts] Unlimited Braid Works (6 solves)
Overview
This is probably hard problem.
Is this commutative or non-commutative?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
(...omit)
n = int(input("Input the security parameter> "))
if n < 16:
print("The security parameter is too small !!")
sys.exit(1)
if (n & 1) == 1:
print("The security parameter must be even !!")
sys.exit(1)
print(f"n: {n}")
## ------------------
## Key Generation
## ------------------
Bn = BraidGroup(n)
gs = Bn.gens()
K = 32
u = random.choices(gs, k=K)
# u must be twisted
if not gs[n // 2 - 1] in u:
u[randint(0, K - 1)] = gs[n // 2 - 1]
u = prod(u)
print(f"u: {prod(u.right_normal_form())}")
al = prod(random.choices(gs[: n//2-2], k=K))
v = al * u * al^-1
print(f"v: {prod(v.right_normal_form())}")
## ------------------
## Encryption
## ------------------
pad_length = 64 - len(flag)
left_length = random.randint(0, pad_length)
pad1 = "".join(random.choices(string.ascii_letters, k=left_length)).encode("utf-8")
pad2 = "".join(random.choices(string.ascii_letters, k=pad_length-left_length)).encode("utf-8")
flag = pad1 + flag + pad2
br = prod(random.choices(gs[n//2 + 1 :], k=K))
w = br * u * br^-1
c = br * v * br^-1
h = hash(prod(c.right_normal_form()))
d = []
for i in range(len(h)):
d.append(chr(flag[i] ^^ h[i]))
d = bytes_to_long("".join(d).encode("utf-8"))
print(f"w: {prod(w.right_normal_form())}")
print(f"d: {d}")
|
The most important part of the given code is above.
This is a non-commutive cryptosystem based on caonjugacy problem on braid group. (The “probably hard” in the description refers to this conjugacy problem).
Let $B_n$ is the braid gorup strands $n$ and $\mathrm{LB}_l,\mathrm{RB}_r$ are left $l$-braids and right $r$-braids in $B_n$.
The secret is $a_l \in \mathrm{LB}_l$ and public keys are $u \in B_n$, $v := a_l u a_l^{-1}$.
Let $m$ is a message and $H\colon B_n \to {0,1}^k$ is a serialize function.
In encryption, server chooses $b_r \in \mathrm{RB}_r$ and calculate $w := b_r u b_r^{-1}$, $d := H(b_r v b_r^{-1}) \oplus m$.
And ciphertext is given as $(w,d)$.
Solution
If we know $a_l$, we can decrypt as follows.
$$
\begin{aligned}
H(a_l w a_l^{-1}) \oplus d &= H(a_l b_r u b_r^{-1} a_l^{-1})\\
&= H(b_r v b_r^{-1}) \oplus H(b_r v b_r^{-1}) \oplus m\\
&= m
\end{aligned}
$$
But we don’t know $a_l$.
This cryptosystem seems proper, but in fact there is a vulnerability in the generation of $u$.
If security parameter $n$ is large, the selections of Artin generators that makes up $u$ is sparse. (Note that if $n$ is too large, the server-side encryption process will take a very long time. So we added to the source code an alarm during of the contest.)
Therefore, let $z$ is the Artin generator across $\mathrm{LB}_l$ and $\mathrm{RB}_r$ then $x_1 \in \mathrm{LB}_l$, $x_2 \in \mathrm{RB}_r$ exists such that
$$
\begin{cases}
u = x_1 x_2 z\\
z \text{ is commutive with } a_l,b_r,x_1,x_2
\end{cases}
$$
with very high probability.
Since
$$
\begin{aligned}
v &= a_l u a_l^{-1}\\
&= a_l (x_1 x_2 z) a_l^{-1}\\
&= (a_l x_1 a_l^{-1}) x_2 z
\end{aligned}
$$and
$$
\begin{aligned}
w &= b_r u b_r^{-1}\\
&= b_r (x_1 x_2 z) b_r^{-1}\\
&= x_1 (b_r x_2 b_r^{-1}) z
\end{aligned}
$$
, the following equiations hold.
$$
\begin{aligned}
a_l x_1 a_l^{-1} &= v z^{-1} x_2^{-1}\
b_r x_2 b_r^{-1} &= x_1^{-1} w z^{-1}
\end{aligned}
$$
Therefore, we can decrypt by $a_lwa_l^{-1} = (vz^{-1}x_2^{-1})(x_1^{-1}wz^{-1})z$.

Solver is here.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
|
from pwn import *
import re
import sys
from Crypto.Util.number import long_to_bytes
sys.setrecursionlimit(30000)
def hash(b):
return hashlib.sha512(str(b).encode("utf-8")).digest()
p = process(["sage", "./server.sage"])
p.sendline(b"50")
log.info(p.recvuntil(b": "))
n = int(p.recvline().strip())
log.info(f"n: {n}")
Bn = BraidGroup(n)
gs = Bn.gens()
def braid_eval(x):
res = gs[0] / gs[0]
x = x.split("*")
for i in x:
res *= sage_eval(i, locals={"gs": gs})
return res
log.info(p.recvuntil(b": "))
u = p.recvuntil(b": ")[:-3].strip()
u = re.sub("s([0-9]+)", "gs[\\1]", u.decode())
u = sage_eval(u, locals={"gs": gs})
log.info(f"u: {u}")
v = p.recvuntil(b": ")[:-3].strip()
v = re.sub("\\\\\n", "", v.decode())
v = re.sub("s([0-9]+)", "gs[\\1]", v)
log.info(f"{len(v)}")
v = sage_eval(v, locals={"gs": gs})
log.info(f"v: {v}")
w = p.recvuntil(b": ")[:-3].strip()
w = re.sub("\\\\\n", "", w.decode())
w = re.sub("s([0-9]+)", "gs[\\1]", w)
w = sage_eval(w, locals={"gs": gs})
# log.info(f"w: {w}")
d = int(p.recvline().strip())
log.info(f"d: {d}")
factors = []
for i in u.Tietze():
factors.append(i - 1)
log.info(f"factors: {factors}")
x1 = gs[0] / gs[0]
x2 = gs[0] / gs[0]
cnt = 0
for i in factors:
if i < (n // 2) - 1:
x1 *= gs[i]
elif i >= (n // 2) + 1:
x2 *= gs[i]
else:
cnt += 1
z = gs[n // 2 - 1]^cnt
print(x1)
print(x2)
print(z)
print(x1 * x2 * z == u)
r1 = v * z^-1 * x2^-1
r2 = x1^-1 * w * z^-1
r = r1 * r2 * z
r = prod(r.right_normal_form())
r = hash(r)
dd = list(long_to_bytes(d).decode())
xx = []
for i in range(len(r)):
xx.append(chr(ord(dd[i]) ^^ r[i]))
flag = "".join(xx).encode("utf-8")
log.info(f"flag: {flag}")
p.interactive()
|

